斐波那契点与斐波那契双曲线
今天所讲内容涉及很多知识内容,但都不难,也很有趣,不妨仔细读一读。
1.预备知识一:斐波那契数列的相关性质
性质A:三个相邻的斐波那契数,外侧两个斐波那契数的乘积,与中间斐波那契数的平方的差,绝对值为1;在中间数的项数为偶数时,外侧两数乘积比中间数的平方大1,在中间数的项数为奇数时,外侧两数乘积比中间数的平方小1。用公式表示就是:
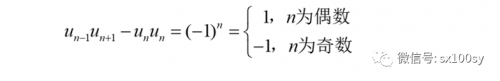
比如,
1,1,2,3,5,8,13,21,34,55,89,144,233,···
(n=4时,2×5-3×3=1; n=5时,3×8-5×5=-1)
性质B:四个相邻的斐波那契数,外侧两个斐波那契数的乘积,与内侧两个斐波那契数的乘积的差,绝对值为1;在四个数的第二个数的项数为偶数时,外侧两数乘积比内侧两数乘积大1,在四个数的第二个数的项数为奇数时,外侧两数乘积比内侧两数乘积小1。用公式表示就是:
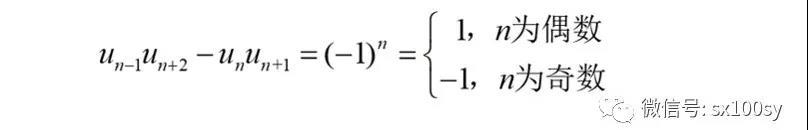
比如,
1,1,2,3,5,8,13,21,34,55,89,144,233,···
(n=4时,2×8-3×5=1; n=5时,3×13-5×8=-1)
这两个性质在后面都要用到。
2.斐波那契点
指(1,0),(1,1),(2,1),(3,2),(5,3),(8,5),(13,8),···这样的点,它们的横坐标依次为斐波那契数,纵坐标先是0,然后再依次是斐波那契数。所以一个斐波那契点的横纵坐标依次是相邻的两个斐波那契数,但横坐标大于纵坐标。
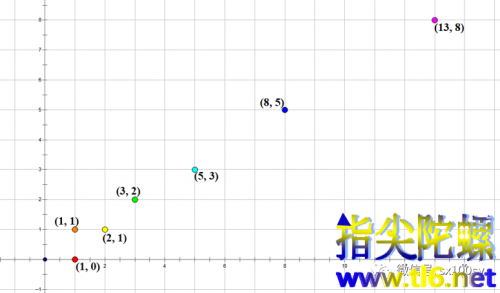
3.斐波那契双曲线
对斐波那契数列的性质A进行变形:
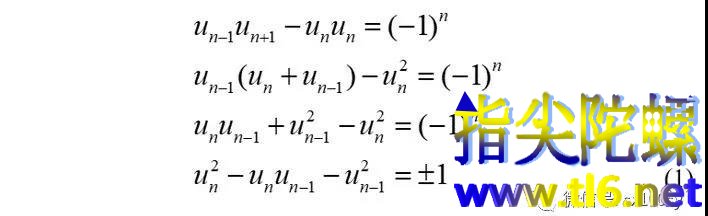
上面最后一式让我们联想到双曲线方程:
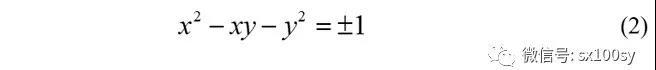
我们画出方程(2)所表示的双曲线(两条双曲线,每条双曲线由两支构成):
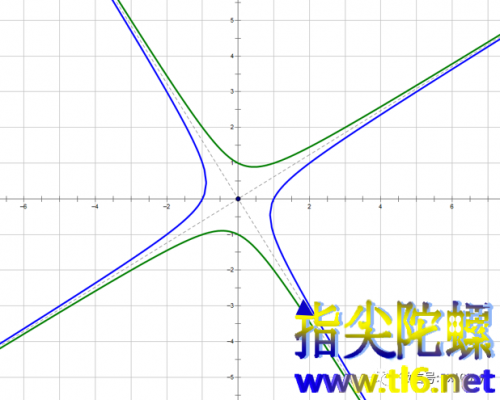
上图中,绿色双曲线对应右端等于-1时的方程;蓝色双曲线对应右端等于+1时的方程。绿色双曲线绕原点旋转90°后,将与蓝色双曲线重合。但是这两条双曲线的对称轴都不是x轴和y轴,而是与x轴和y轴有一个角度。这是因为双曲线的方程中有xy项。上图中还画出了这两条双曲线的公共渐近线,其中一条渐近线的斜率为黄金数0.618···[用根式表示为(√5-1)/2]。
比较方程(1)和(2),很容易发现,满足方程(1)的一对斐波那契数(un,un-1)一定满足方程(2)。而(un,un-1)正是斐波那契点的坐标。所以,可以有结论:斐波那契点一定位于上图所示双曲线上。这个结论还有些粗糙。其实,因为斐波那契点的横纵坐标都大于等于0,所以,斐波那契点全都位于下图所示的第一象限部分的双曲线上。再由上段所说的90°旋转对称性,点(un,un-1)及其90°旋转对称点(-un-1, un)、(-un,-un-1)、(un-1,-un)就全都位于这两条双曲线上。
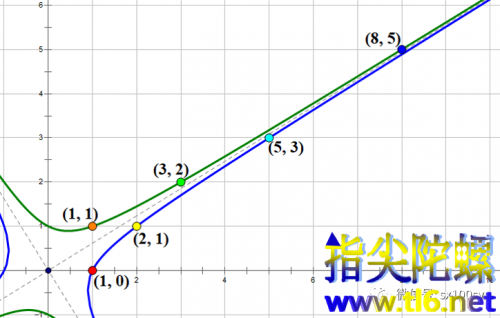
以上这些点都是格点,它们都位于双曲线上。但我们还不能确定是否有其他不是斐波那契点的格点,它们的坐标也满足方程(2),也就是说,我们还不能确定由方程(2)表示的双曲线上是否有不是斐波那契点的格点。下面我们就要证明,除斐波那契点外,没有其他任何一个格点位于方程(2)所表示的双曲线上。然后,我们就可以顺理成章地给这样的双曲线取一个名称——斐波那契双曲线。
证明前,需要先掌握下面两个预备知识。
4.预备知识二:皮克定理
皮克定理是针对格点多边形的,且多边形没有边界交叉。用I表示多边形内部格点数量,B表示边界上的格点数量。则多边形面积S由下面的公式给出:
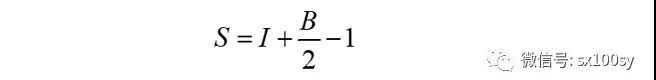
比如下图所示格点多边形:
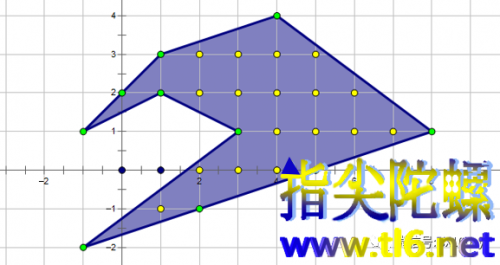
观察,它一共有17个内部格点(黄色),10个边界格点(绿点;可以是顶点,也可以是边上的点),所以,根据皮克定理,有
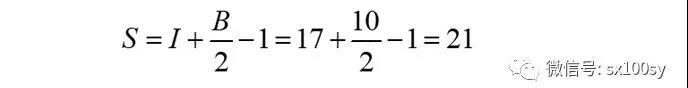
5.预备知识三:三角形面积的行列式公式
已知三点A、B、C的坐标分别是(x1,y1)、(x2,y2)、(x3,y3),那么三角形ABC的面积S用行列式表示的公式是:
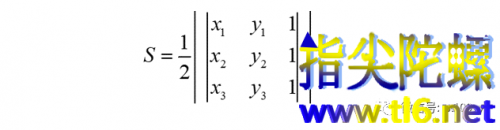
其中内层两竖线“| |”表示行列式,外层两竖线“| |”表示绝对值。在A、B、C三点不在一条直线上(否则面积为0)的情况下,当A、B、C三点逆时针排列时,行列式为正值,当A、B、C三点顺时针排列时,行列式为负值。注意,不能少了乘以1/2。
6.前面已经证明了所有斐波那契点及它们分别旋转90°、180°、270°所得到的点,全都位于这两条双曲线上。下面我们根据以上这些预备知识,来证明下面的结论:位于这两条双曲线上的点如果是格点,那它一定是斐波那契点或它们旋转90°、180°、270°所得到的点(或者说,这两条双曲线穿越所有斐波那契点及它们分别旋转90°、180°、270°所得到的点,把其他一切非斐波那契点的格点留在这两条双曲线之外)。这时,我们就可以给这两条双曲线起个名字,叫斐波那契双曲线。
我们在第一象限内进行证明。如下图所示,每相邻的三个斐波那契点连接出一个格点三角形。比如图中橙色三角形是由点(1,0),(1, 1),(2, 1)构成的格点三角形;粉色三角形是由点(1, 1),(2, 1),(3, 2)构成的格点三角形;······
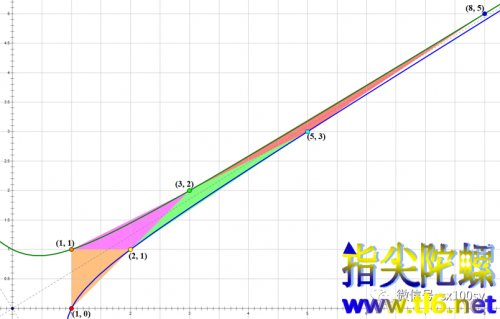
我们先来证明所有这些三角形的面积都是1/2。上图中,橙色和粉色三角形的面积为1/2是容易看出来的,但绿色三角形面积为1/2就不那么容易,所以,需要用公式。我们要用到前面的预备知识三:三角形面积的行列式公式。三个连续的斐波那契点的坐标可以写成:
(un,un-1),(un+1,un),(un+2,un+1)
(其中n=1,2,3,···。补充定义u0=0。)
那么,以这样三个连续斐波那契点为顶点的三角形的面积就是:
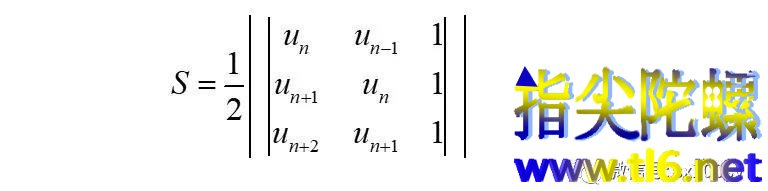
按第三列展开行列式,得
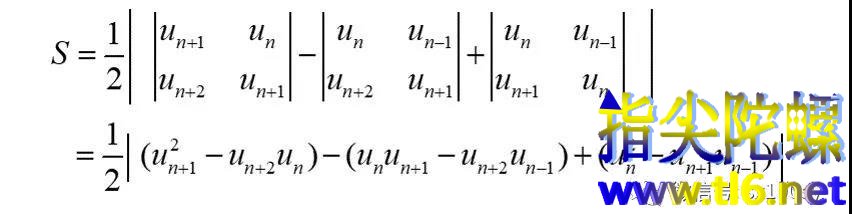
根据前面预备知识一中的性质A,不管n是奇数还是偶数,上式中绝对值内部的第一项(指括号内)和第三项,一定是一个为+1,一个为-1。所以,两者互相抵销。于是,绝对值内部还剩余一项:
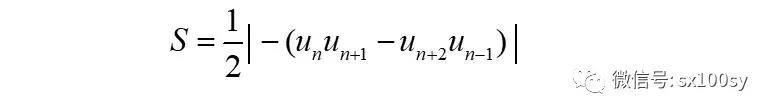
根据前面预备知识一中的性质B,上式绝对值中括号内的值为1或-1,所以,上式就等于1/2,即
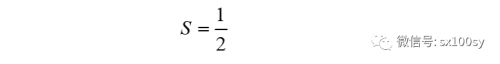
有了上面每个三角形的面积都为1/2这一结论,我们下面就来应用皮克定理证明双曲线上不存在其他格点。
皮克定理为:
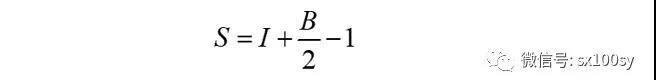
上式左端S=1/2。边界点的个数B至少是3。那么,上式右端“内点个数I不可能大于0”和“B不可能大于3”这两者,如果有一个被破坏,都将导致右端大于1/2。矛盾。所以,只能I=0,B=3。即三角形没有内点,边界点也只有三个顶点。

观察发现,每个这样的三角形都覆盖住了双曲线的一段,那么这一段上就没有格点(因为无内部格点)。又因为所有这些三角形一起,完全覆盖了双曲线位于直线x=1右侧全部,而位于x=1和y轴之间那段双曲线也只有(0,1)这一个格点,但它是斐波那契点(1,0)旋转所得。所以,双曲线上一定不存在除斐波那契点以外的其他格点。于是,我们就证明了我们本期内容所要证明的结论:
在由前面方程(2)所表示的双曲线上,除斐波那契点及它们分别旋转90°、180°、270°所得到的点外,没有其他格点。