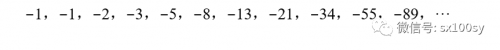斐波那契数列的大性质
今天讲斐波那契数列的一条很大的性质。说它大,是因为它涵盖了我们以前知道的多条性质。
这个大性质就是下面这个公式[其中的ui (下标i是正整数)都是斐波那契数]:
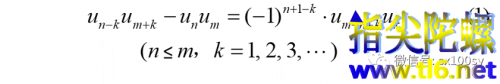
它说的是,斐波那契数列中任意两项的乘积与和它们等距离的另外两个斐波那契数的乘积之间的关系。下面我们就一一举例说明。先把斐波那契数列放在这里供参考:

1. 若(1)式中n=m,k=1,则有
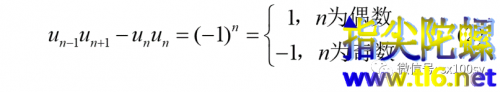
这个不就是我们之前讲过的隐藏在那个著名几何谬误背后的秘密么!
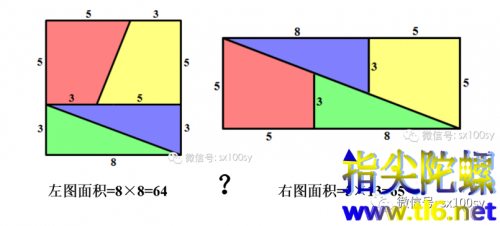
具体来说,就是n=6时的情况:
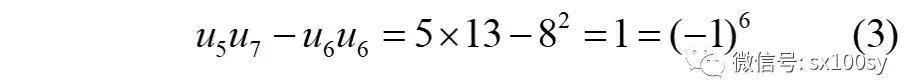
我把右图放大,就可以发现有一个面积为1的缝隙。
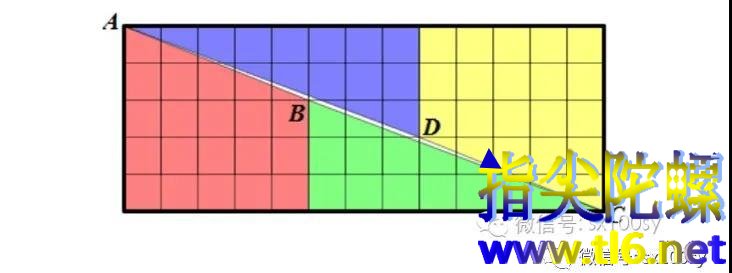
(有关这个几何谬误的具体解说,可阅读我之前的文章。)
2.若n比m小1,即n和m是连续两个正整数,那么m-n=1。仍然让k=1。那么由公式(1),有
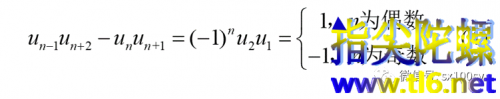
这就是说,四个相邻的斐波那契数,外侧两个斐波那契数的乘积,与内侧两个斐波那契数的乘积的差,绝对值为1;在四个数的第二个数的项数为偶数时,外侧两数乘积比内侧两数乘积大1,在四个数的第二个数的项数为奇数时,外侧两数乘积比内侧两数乘积小1。比如:8,13,21,34这四个连续的斐波那契数,第二个数13为斐波那契数列的第7项,是奇数项,所以,外侧两数乘积比内侧两数乘积小1:8×34-13×21=272-273=-1。确实。

3.若n比m小2,即n和m中间隔着一个数,这时m-n =2。依然让k=1。那么由公式(1),有
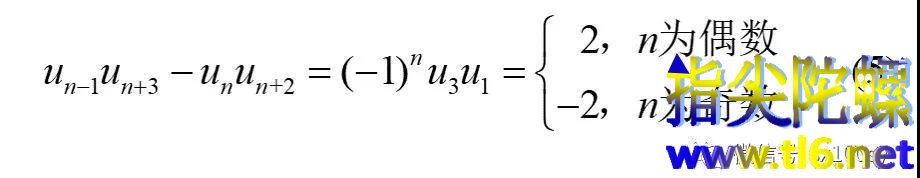
也就是说,连续的五个斐波那契数,外侧两个数的乘积与次外侧两个数的乘积之差的绝对值为1。是1还是-1,视第二个数的项数是奇数还是偶数而定。比如8,13,21,34,55这五个连续的斐波那契数。

五连数中,第二个斐波那契数(项数对应公式中的n)是13,是第7项,即奇数项,所以8×55-13×34应该等于-2。计算一下,确实如此:
8×55-13×34=440-442=-2。
4.上面给出了几个简单的例子。下面我们将更加关注(1)式的右侧,因为右侧也有斐波那契数存在。首先,我们控制m和n都不变,所以m-n也不变。比如m=6,n=5,所以m-n =1。于是,(1)式
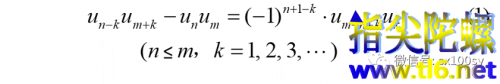
就变为具体的(6)式:
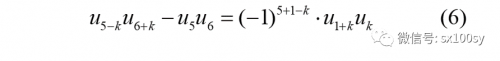
我们观察k的变化对差值的影响,感受一下变化规律(是正还是负,大小的变化),并体会这个公式的通用性。
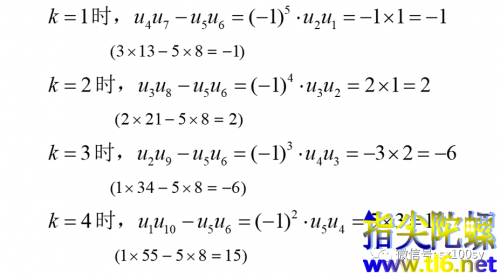
发现左侧的差值一负一正交替。大小为连续两个斐波那契数的乘积,且逐渐增加。
通过下图可直观感受上面的结果。

上面讲了几个比较简单常用的性质与本期所讲这条大性质的关系。下面我们再利用这个大性质给您变个戏法。
5.我将根据这个有关斐波那契数列的大性质,去构造斐波那契数列。很好玩儿!大性质先放在这里:
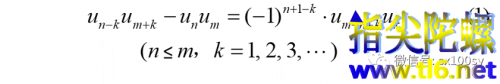
在上式中固定n为某个正偶数。并固定k=1。从而n-k = n-1也是固定的。这就相当于上式中左侧四个斐波那契数中的两个是固定的(其实是较小的两个是固定的)。然后,我们让m变化,m可以最小等于n,然后连续增加1。我们再看一下(1)式的右侧。(-1)的指数n+1-k = n,是确定的。又因为我们取的n为正偶数,所以,(-1)的n次方为正1,所以(1)式右侧都为正。右侧两个斐波那契数的乘积中,uk=u1=1,显然是确定的。另一项um-n+k=um-n+1。当m=n时,它等于u1=1,然后,随着m逐一增加,它也将从u1变为u2,并逐一变成u3,u4,···。这不就是斐波那契数列么!
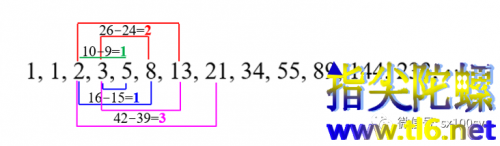
上面我从公式的分析上,构造出了一个斐波那契数列。下面我用图来进行展示,更加有趣。如下图所示,生成的各项为:
第一项为绿色的1,
第二项为蓝色的1,
第三项为红色的2,
第四项为粉色的3,
第五项为2×34-3×21=68-63=5,
第六项为2×55-3×34=110-102=8,
第七项为2×89-3×55=178-165=13, ············
一直成生一个斐波那契数列。
若本条中的n取为正奇数,其他不变,我们将构造出一个负斐波那契数列: