斐波那契数列与音乐节拍
以前讲过很多例子,它们的模型都是斐波那契数列。今天再讲一个,我们一起来看看是怎么回事。这个例子与音乐有关。斐波那契数列真是丰富多彩。
涉及音乐的节拍。设一个短音为一拍,用一字线“一”表示;一个长音时长为短音的两倍,为两拍,用二字线“一一”表示。用这两种声音奏出一小节的声音。那么具有n拍(n=1,2,3,···)的一小节有几种不同的节奏类型?我们边举例子边说明什么是节奏类型。显然,n=1即一小节只有1拍时,声音只能用一个短音奏出,即“一″,所以只有一种节奏类型。n=2即一小节有2拍时,声音可以用两个短音奏出,也可以由一个长音奏出,即

所以n=2时有两种节奏类型。
当n=3即一小节有3拍时,我们怎么考虑问题以确定有几种节奏类型?我们知道,一小节结束前可以是一个短音,也可以是一个长音。(1)在结束前是一个短音的情况下,这个短音之前已经奏出了两拍,这两拍就具有前面讲过的两种节奏类型;(2)在结束前是一个长音的情况下,它占据了两拍,三拍中的第一拍只能是一个短音,也就是一种节奏类型。所以,三拍时一共是三种节奏类型(即2+1=3)。如下图所示:
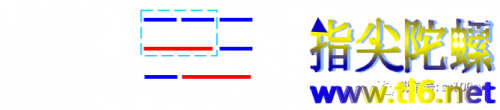
当n=4即一小节有4拍时,同样地考虑结束前分别是一个短音还是一个长音的两种情况:结束前是一个短音时,前三拍就是n=3的情况;结束前是一个长音时,前两拍是n=2时的情况。所以,四拍时一共有3+2=5种节奏类型。
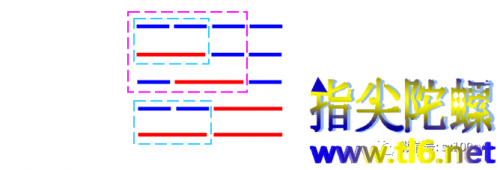
继续下去,就是下面这幅图。它是n=5即一小节有5拍时的情况,共有节奏类型5+3=8种。
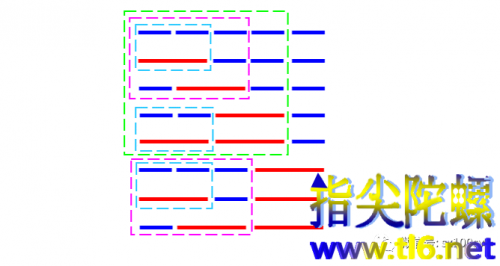
这不就是斐波那契数列的递归关系么!即一个n拍所拥有的节奏类型,就等于一个n-1拍所拥有的节奏类型加上一个n-2拍所拥有的节奏类型。所以,我们就得到了这个节拍问题的节奏类型的一个数列:
1,2,3,5,8,13,21,34,···
这个数列缺少斐波那契数列的第一项,其他项完全一样。
从下图我们可以看出这个数列的走向,很有意思:
当然了,不是每种节奏类型都好听!这里只是数学上的研究,实际音乐上使用什么节奏型,可能又是另一回事。但音乐与数学是有联系的!除节奏上与数学有关外,音高也与数学有关。
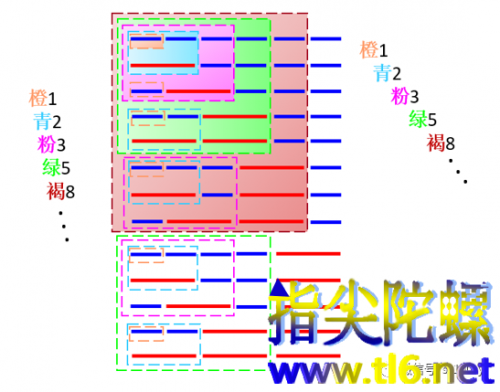
这个问题与爬楼梯问题是完全同构的。所谓爬楼梯问题是这样说的:有一楼层共有n级台阶,一个人一次可以迈上一级台阶,也可以一次迈上两级台阶,不准后退。问这个人从楼层下面爬到楼层上面,一共有多少种不同的爬楼方式?下图是n=4时的情况,一共有5种爬楼方式:
0→1→2→3→4(红+橙+绿+青);
0→1→2→4(红+橙+粉);
0→1→3→4(红+褐+青);
0→2→3→4(蓝+绿+青);
0→2→4(蓝+粉)。
