帕斯卡三角形和斐波那契数列
下图就是著名的帕斯卡三角形的前8行。它的一个重要性质就是:两腰上的数字全都是“1”,中间的数字,是它的肩上两个数字之和,即它的左上方数字和右上方数字之和。比如,6=3+3;15=5+10或15=10+5。
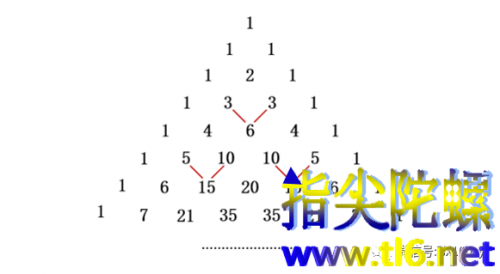
上图中您看出斐波那契数列在什么地方吗?似乎不太容易看出来吧。对,斐波那契数列没有直接出现在上面帕斯卡三角形中。为了让斐波那契数列显现出来,我们需要给上面的帕斯卡三角形做适当的变形——让45度角斜线(“/”方向)上的数字竖立起来,即让左腰上的一串“1”与水平线垂直,其他斜线上的数字跟随着也竖立起来。于是原来的等腰三角形的两腰不再相等,而是变成一个直角三角形——原来的一腰变成一直角边,另一腰变成斜边。如下图所示。

于是,前面说到的那条性质,在这里变成:左侧直角边上的数字全是“1”,右侧斜边上的数字也全是“1”。中间的数字是它左斜上方数字与正上方数字之和。如上图所示。比如第8行第3个数21=6+15;第8行第4个数35=15+20。
然后,用45度角的斜线(“/”方向)把数字串起来,则每条斜线上的数字之和就是一个个的斐波那契数。如下图所示。
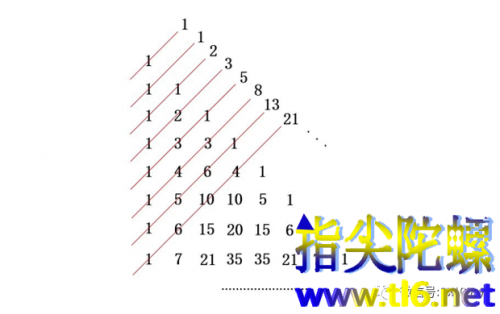
我们从图中可以看出,这些斜线上数字之和,从左上到右下正好构成斐波那契数列:
1,1,2,3,5,8,13,21,34,55,···
我们知道,斐波那契数列从第3项开始,它等于前面两项之和,这是斐波那契数列的递推关系。我们可以从下图中清楚地看出这一递推关系——任何一条斜线上的数字之和都等于它上面两条斜线数字之和的和(第1条斜线上数字之和为1,第2条斜线上的数字之和也为1)。下图以21=13+8为例来加以说明。
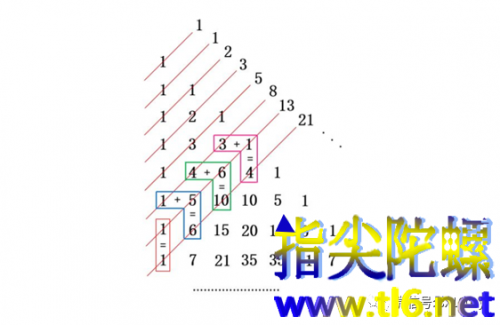
上图中,第8条斜线(即其数字之和为21的斜线)的第1个数“1”与上面一条斜线的第1个数“1”相等(红框);第8条斜线的第2个数“6”是第7横行中第2个数,它等于其正上方的数“5”与左斜上方的数“1”之和,而这两个加数一个是第7条斜线中的第2个数,一个是第6条斜线中的第1个数(图中蓝框)。······,类似的递推关系如上图绿框和紫框所示。最终可以看出,第8条斜线上所有数字之和可以转换成其上方的第7条斜线和第6条斜线上的所有数字之和。也就是说,从第3条斜线开始,它串起的数字之和等于“位于其上面第1条斜线串起的数字之和”加上“位于其上面第2条斜线串起的数字之和”。
在往下讲之前,还需要知道下面的情况。数学就是这样,越研究越精细,越深入,越有趣。我写的东西,力争做到相关方面应讲尽讲。但又不失系统性和严谨性。
上面那张图显示的是F8=F7+F6,即第偶数序号的F数或第偶数条斜线上数字串之和,等于它前面两条斜线数字串之和的和。我们前面已讲了,前后一奇一偶两个连续序号的斜线,串起来的数字的个数相等(比如F7与F8都是由相同个数的数字相加而成);而前后一偶一奇两个连续序号的斜线,串起来的数字的个数就是前者比后者小1(比如F6这条斜线就比F7这条斜线串起的数字个数少1)。下图给出F9=F8+F7的图示,与前面F8=F7+F6的图示有一些不同,请您仔细辨识,这将为后面的证明做个铺垫,让您有些感性的认识。
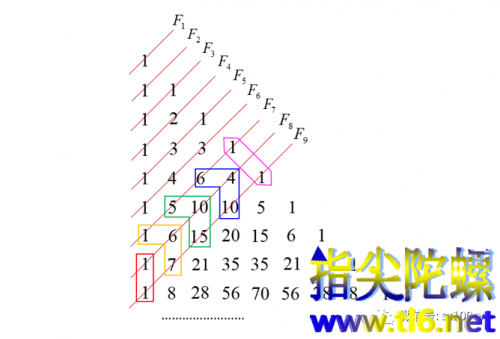
(注意:错位相加,即
1 + 6 +10 + 4
+ 1 + 5 + 6 + 1
= 1 + 7 +15 +10 + 1
=34
但上面的叙述仍然只是一种感观上的,我们还是需要从数学上对帕斯卡三角形中存在这样的斐波那契数列进行严格的证明。首先,我们把帕斯卡三角形写成组合数的形式:
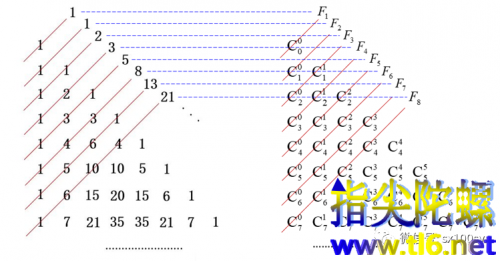
单独观察上图中的右图,发现,从上到下,第1、2条斜线串起的数字的个数都是1。第3、4条斜线串起的数字的个数都是2。......第2k-1和第2k条斜线所串起的数字的个数都是k。这是帕斯卡三角形的特点。再以第8条斜线为例,看一下F8所串起的4个数字是哪4个数字。
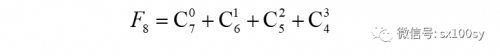
从上式发现,它是由一些组合数相加而得,每个组合数的C的下标与上标之和都等于(8-1)=7,并且因为上标一定小于等于下标,所以,这样写下来,就只有4项。
当斜线序号即F数的下标为偶数时,组合数上下标之和就为奇数,所以,按下标从大到小的顺序排列这些组合数,最后一个组合数的上标一定比下标小1。当斜线序号即F数的下标为奇数时,组合数上下标之和就为偶数,所以,按下标从大到小的顺序排列这些组合数,最后一个组合数的上标一定等于下标。比如F7:
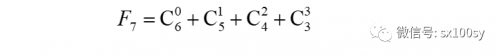
所以,我们可以归纳出第n条斜线上数字之和,即第n个F数(斐波那契数的简称)Fn的通项公式:

其中

上式中“[ ]”表示取整,比如[3.5]=3,[3]=3,[π]=3。举例,n=6时,
[(n-1)/2]=[(6-1)/2]=[2.5]=2,
(n-1)-[(n-1)/2]=(6-1)-2=3
所以,
F6=C(5,0)+C(4,1)+C(3,2)=1+4+3=8
(上式中,C(n,m)就是从n中取m个的组合数。)
下面用数学归纳法证明按照上面的通项公式得到的数列就是斐波那契数列。首先,第1条斜线上的数字之和等于C(0,0)=1=F1;第2条斜线上数字之和等于C(1,0)=1=F2。第3条斜线上的数字之和等于C(2,0)+C(1,1)=1+1=2=F3,所以F3=F2+F1。下面来证明对任意的n>1,都有Fn+1=Fn+Fn-1。假设n为偶数,即n=2m(n为奇数的情况类似)。于是

上式最后一行下面要用到。

上式最后一行下面也要用到。
把上面两个结果写得完整一些:
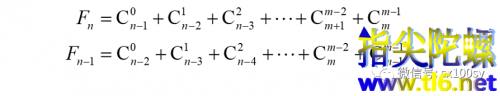
两式错位相加,得:
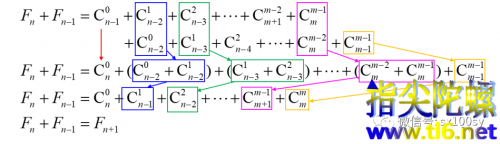
所以,得证。你是不是觉得数学很美妙!