斐波那契数列的性质都有那些?
斐波那契数列的性质特别多。真是一个神奇的数列!今天就给您介绍这么几条。
第一组3条:
性质1:斐波那契数列前n项和等于第n+2项减1。用公式表示就是:
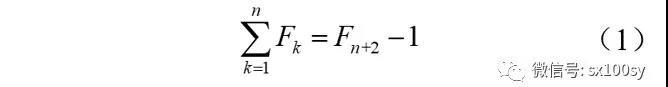
比如,前8项和:
1+1+2+3+5+8+13+21=55-1=54。
(第9项34没有出现。但其实它是最后两项的和。)
这条性质不难证明,如下:

相加,得
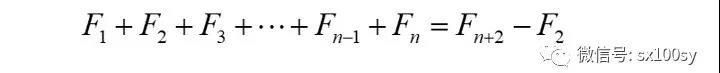
即
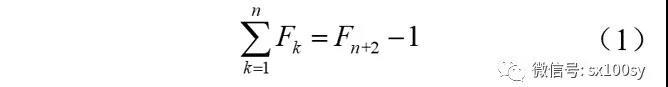
性质2:前n个项数为奇数的斐波那契数之和等于第2n个斐波那契数,或者说,第偶数项的斐波那契数等于其前面所有奇数项斐波那契数之和。用公式表示即为:
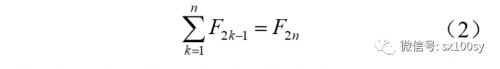
不用连加符号,更加直观一些:
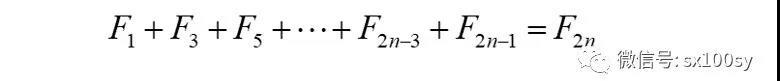
比如,
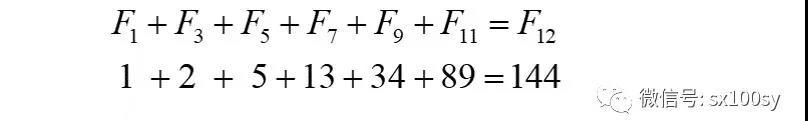
证明不难,仍可采用“拆项、抵消”的方法。对照上面不用连加符号的公式,心里想一下即可想通。
性质3:前n个项数为偶数的斐波那契数之和等于第2n+1个斐波那契数减1,或者说,第奇数项的斐波那契数等于其前面所有偶数项斐波那契数之和再加1。用公式表示即为:
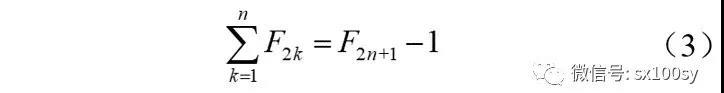
比如
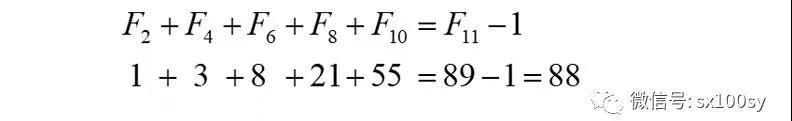
证明不难。考虑性质1即下面的公式(1')和性质2即下面的公式(2),再考虑下面的(4)式,用公式(1')减去公式(2),便可得出性质3的公式(3)。
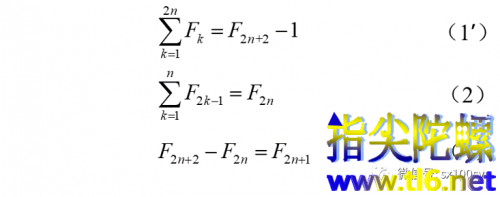
第二组3条:
性质1:前n个斐波那契数的平方和等于第n个斐波那契数与第n+1个斐波那契数的乘积。用公式表示就是:
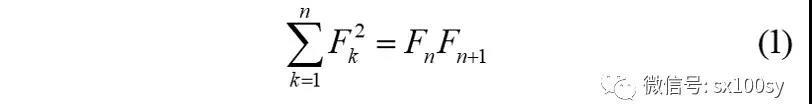
这样一来,我们求前9个斐波那契数的平方和,就不必每个数平方后再相加,而只需求两个数的乘积即可,简单了很多。又因为一个斐波那契数等于其前面两个斐波那契数之和(斐波那契数的定义),所以,我们只需求出这9个斐波那契数的最后两个之和,即F10,再让这个和乘以最后一个斐波那契数F9即可。比如:
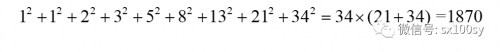
这个性质即公式(1)的证明很简单:

以上n个式子相加,右端出现两两抵消的情况,最后就剩下一项,就是我们想要的结果。
性质2:斐波那契数列中前2n个相邻两项乘积之和,等于第2n+1个斐波那契数的平方再减1。即
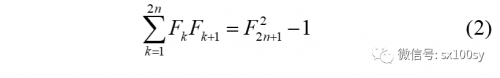
(注意,(1)我们单说“项”时是指斐波那契数列的项,比如F5;上式左侧两相邻项的乘积,我们可以称其为“乘积项”,比如F2F3,但不称其为“项”,以免与斐波那契数列的“项”混淆。(2)上式左边共有2n(偶数)个乘积项,但因为每一乘积项都是连续两个斐波那契数的乘积,所以,一共涉及前2n+1个斐波那契数。)
举例:

我们要求前10个乘积项之和,但涉及前11个斐波那契数(如上表),所以结果就是F11的平方再减1。
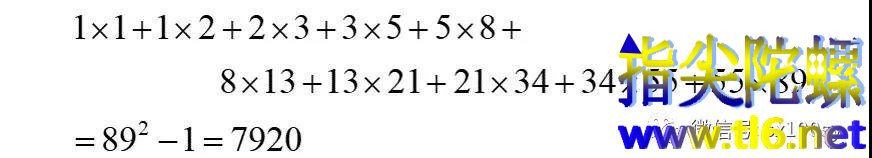
(注意,性质2中左侧求乘积项之和时,一定是偶数个乘积项之和。右侧平方数中一定是斐波那契的奇数项的平方,其实就是左侧序号最大的那个斐波那契数的平方。否则性质不成立。比如,若是前5个乘积的和,则左侧为1+2+6+15+40=64,而右侧为8^2-1=64-1=63。两者不相等。我们从下面的证明过程也可以看出左侧一定是偶数个乘积项之和,才能两两配对成功。求和符号上限2n已经说明了求和的数量是偶数。)
下面的证明过程:

性质3:斐波那契数列中前2n-1个相邻两项乘积之和,等于斐波那契数列第2n项的平方。即:
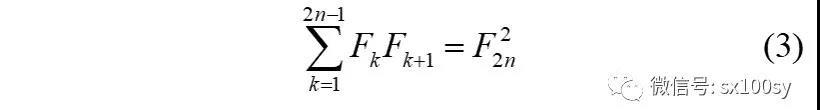
上一条中求和号上限为偶数,本条性质就来解决奇数的情况。左侧涉及2n个斐波那契数,右侧是其中最大的那个斐波那契数的平方。证明不难,把上一条的证明稍加改造即可。如下:
