双曲线切线与渐近线围成的三角形面积不变
(1)圆锥曲线的内与外。如下图所示,阴影区城为内。
(2)在双曲线外一点向双曲线可以引两条切线。若这点位于双曲线对称中心,则两条切线就是双曲线的两条渐近线。所以,从非对称中心一点所引两条切线与两条渐近线,可以看成四条切线。这四条切线可以构成双曲线的一个外切四边形。
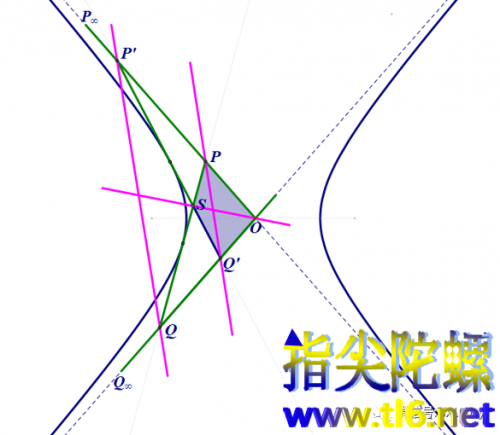
具体来说,如上图所示,直线PQ与双曲线的左支相切,直线P'Q'也与双曲线左支相切。点P和Q是切线PQ与两条渐近线的交点,点P'和Q'是切线P'Q'与两条渐近线的交点。设PQ和P'Q'的交点为S。这样,包括两条渐近线在内的四条切线围成一个四边形OPSQ'。注意,在圆锥曲线是圆或椭圆(比如上期的例2)时,明显可以看出外切四边形确实把圆或椭圆“包在里面”。但在双曲线的情况,因为双曲线延展到无穷远,感觉不可能有四边形能够“包”住它。但是,正像在球面上,我在我的外围画一个半径一米的圆,我若认为我是在圆外,则球面上除我所在这个小圆以外的绝大部分区域就被这个圆包围,成为圆内。事物都是相对性。所以,在这里的双曲线的情况下,我们未尝不可认为上面这个小四边形也把双曲线包围住。
好的,我们继续。这时,就出现了一个完全四边形OPSQ'P'Q,它有三条对角线:直线OS,直线PQ'和直线P'Q。它们将围出一个在上一期讲过的所谓的“自配极三角形”。根据自配极三角形的意思,直线PQ'和P'Q的交点是直线OS关于双曲线的极点。

我们知道,从圆锥曲线外部向曲线引的两条切线的两个切点的连线,就是这个点关于曲线的极线,所以,从对称中心O发出的两条切线(即两条渐近线)与双曲线的两个交点的连线就是对称中心O的极线。但由于渐近线与双曲线的交点在无穷远,所以,两个切点就是两个无穷远点,两个切点的连线就是无穷直线。我们用P∞和Q∞表示这两个切点,用P∞Q∞表示无穷直线,则无穷直线P∞Q∞就是点O关于双曲线的极线。
我们来看极线OS与它的极点。极线OS上的任意一点向双曲线所引的两条切线,所得两个切点的连线也一定经过OS的极点。
那么,前面三段的结尾处的三个加粗结论说明,无穷直线P∞Q∞一定经过直线PQ'与P'Q的交点。就是说,直线PQ'与P'Q在无穷远点相交。
(若有不太明白之处,可与上一讲对照阅读。)
根据欧氏几何,直线PQ'与P'Q平行。那么,再来看下面的图,两条粉色直线PQ'与P'Q平行。那么,由蝴蝶定理,三角形SPP'的面积就等于三角形SQQ'的面积。两者都加上四边形OPSQ'的面积,就得到三角形OPQ与三角形OP'Q'面积相等。也就是切线PQ与两条渐近线所围三角形的面积等于切线P'Q'与两条渐近线所围区域的面积。也就是说,双曲线切线与两条渐近线所围三角形的面积不变,或者说是常数。

上面所说的三角形SPP'的面积等于三角形SQQ'的面积,也可以说成过双曲线外一非对称中心的点向双曲线所引两条切线,被两条渐近线截出两个面积相等的三角形。
(蝴蝶定理很简单,根据的是同底等高的两个三角形面积相等,再都减去它们的公共部分,就得到两个像蝴蝶的两翼一样的三角形的面积相等。)