等轴双曲线内接三角形的垂心轨迹是什么?
发布时间: 浏览: 次 作者:www.tl6.net
渐近线互相垂直的双曲线叫做等轴双曲线。若我们以x轴和y轴为渐近线,那么,等轴双曲线的方程就是xy=k(常数)。从函数的角度看,它就是反比例函数y=k/x。
取k=1,我们在直角坐标系中画出反比例函数y=1/x的图像,如下图所示。在等轴双曲线上任取三个点A、B、C。以三个点为顶点作一个三角形ABC。如下图所示。

作这个三角形的垂心P。我们发现,这个垂心P正好位于双曲线上。
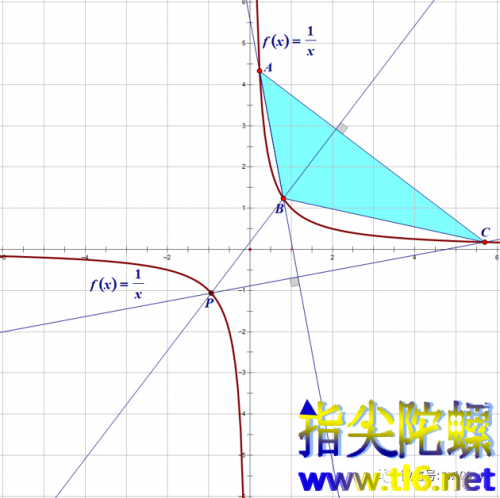
下图是改变了三个顶点的位置,发现点P位置变了,但仍然位于双曲线上。
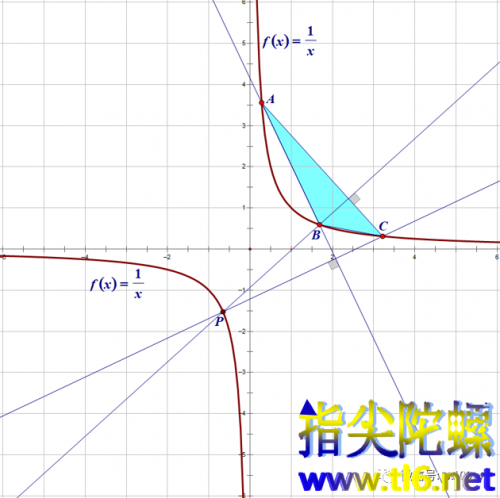
我们把三个顶点置于双曲线两支当中,发现,垂心仍然位于双曲线上。
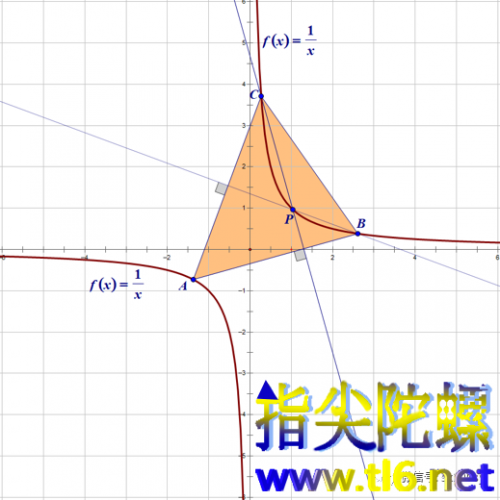
下面我们用代数方法证明点P的轨迹就是等轴双曲线本身。
设三个顶点A、B、C的坐标分别为(a,k/a),(b,k/b),(c,k/c)。于是,直线AB的方程为
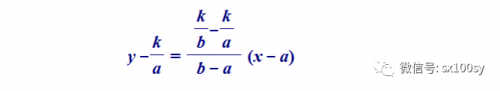
即
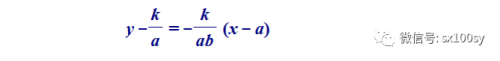
它的斜率为-k/ab。所以,它的垂线的斜率为ab/k。从而过点C的AB边上的垂线方程为

同理,可得BC边上的垂线方程为

求出两条垂线的交点即三角形的垂心坐标为
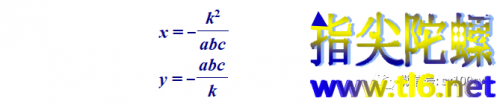
很容易看出,垂心的横纵坐标的乘积为

即这个垂心的横坐标或纵坐标都依赖于三个顶点的坐标,且可以取到除0以外的任何值。但横、纵坐标的乘积却是常数k。这就说明,垂心坐标满足等轴双曲线方程xy=k。垂心的轨迹就是原来的等轴双曲线本身。很神奇!

若三角形的三个顶点都位于双曲线的一支上,则垂心一定位于另一支上。若有两个顶点位于同一支上,另一顶点位于另一支上,则垂心位于两个顶点所在的那一支上。
这个问题叫做布里安香-彭色列双曲线问题。这个问题只适用于等轴双曲线。