用积分方法计算牟合方盖的体积

(图片来源于网络)

(图片来源于网络)
下图所示餐桌罩有一些也是做成牟合方盖样子的(也是只用半个牟合方盖)。

(图片来源于网络)
用更加接近数学的语言来描述牟合方盖,是这样的:有两个横截面直径相等的圆柱,它们互相垂直地互相交叉(互相穿过对方,且中轴线相交),那么,两者公共部分就是所谓的牟合方盖。
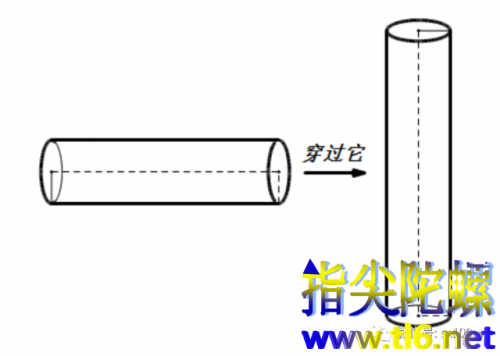
整个牟合方盖是什么样子的呢?是这样的:
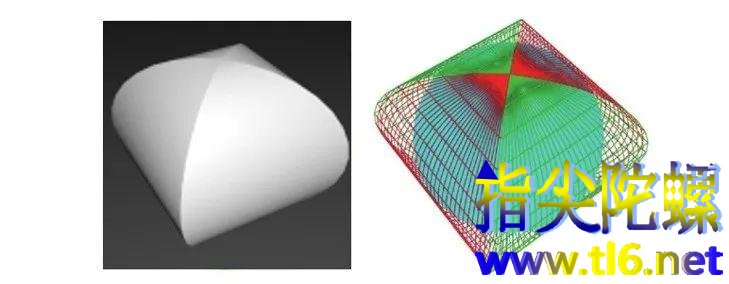
(图片来源于网络)
(2)那么,牟合方盖体积怎么计算?
在中国,牟合方盖很早就提出来了,中国数学家用了一个巧妙的办法求出了牟合方盖的体积。具体来说,这是怎么做到的呢?
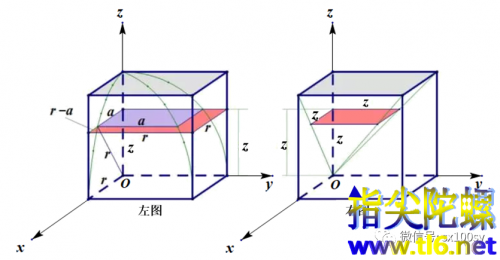
下图中的左图为牟合方盖的八分之一。右图为同大小正方体内的一个倒四棱锥。
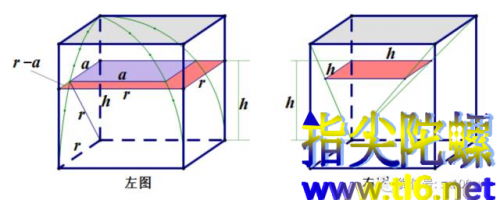
从图中容易发现下面的关系:
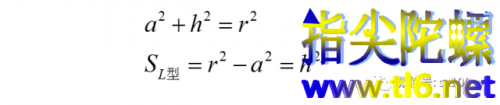
而右图倒四棱锥同高度的截面面积为:
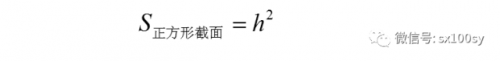
根据祖暅原理[ 也叫刘祖原理(刘指刘徽,祖指祖暅),等幂等积定理(幂指截面面积,积指立体体积);国外叫卡瓦列里原理],上图中正方体与牟合方盖的八分之一之间空隙的体积与倒四棱锥的体积相等。而倒四棱锥体的体积为
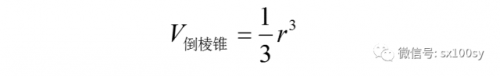
所以,八分之一牟合方盖的体积等于正方体的体积减去倒四棱锥的体积:
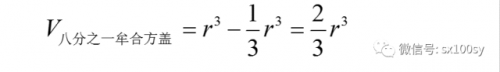
那么,整个牟合方盖的体积就是:
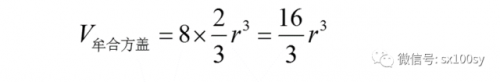
(3)下面我们用现代数学中的积分方法来求牟合方盖的体积。给上图添加坐标系,如下:
求八分之一牟合方盖的体积再乘以8,就得整个牟合方盖的体积:

上面的积分变为两个积分的差,正好反映了正方体体积与倒四棱锥体积之差。与几何上的直观是多么的一致!我前面说中国古代数学家很伟大,您相信了吧!
(4)数学家波利亚在《怎样解题》一书中让我们努力挖掘公式背后的实际意义!确实是这样的!我们从上面的积分中挖掘出了中国古代数学中求牟合方盖体积的精妙方法。两者原来是一回事。古代方法直观、明白、有趣、感性;积分方法抽象、简洁、理性,但确实威力巨大(积分方法似乎绕过了“等幂等积定理”,直奔结果)。古代数学伟大,近代数学微积分更加厉害!
(5)有了牟合方盖的体积,我们再来求球的体积。
下图所示是由沿x轴方向的圆柱与沿y轴方向的圆柱正交后公共部分(即牟合方盖)的上半部分。只画一半,因为另一半与这一半对称。图中绿色阴影是x轴方向圆柱面的一部分,蓝色阴影是y方向圆柱面的一部分。因为柱面是直纹面,所以可以看出,沿水平方向(平行于xy面)切割它,所得一定是正方形。
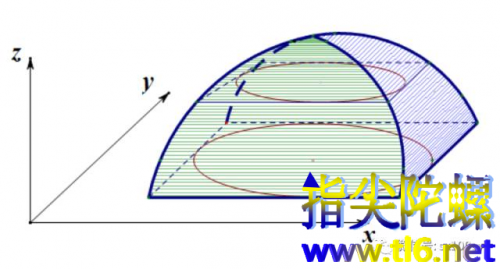
我们设想一下,两个圆柱体在相交处是打通的,那么,把一个直径刚好等于圆柱底面直径的球分别从这两个圆柱中间放入,像打炮一样,让它沿直线运动,那么球一定都是正好沿着圆柱的内壁从一头装进去,从另一头发射出。中间有这么一个位置,球若处于这个位置,它就正好挡住了视线,使我们不能从任何一个圆柱的一端从内部看到另一端。所以,如果当这个球正好位于这个位置时,我们再把两个圆柱面位于对方内部的部分补上,那么,所补部分正好就是我们所要求其体积的那个空间一一牟合方盖。它把这个球围在了里面,并使得球不能动弹,即球与牟合方盖是内部相切的。
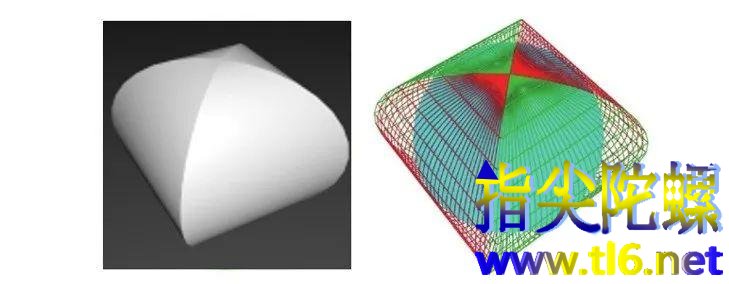
前面说过用水平面切割这个牟合方盖,切平面与牟合方盖的交线是一个正方形,但如果切割时球还在里面,则切割平面与球的交线就是下图中的圆。这个圆位于正方形内部与正方形四边都相切。(下图相当于牟合方盖的上半部分。)

球与牟合方盖虽然是相切的,但之间是有空隙的(因为切出的正方形与圆之间有空隙)。
对于每一水平切片,都是由一个正方形和它的内切圆构成。正方形是牟合方盖的横截面,圆是球的截面。正方形与圆之有空隙,这个空隙就是牟合方盖与球之间空隙的来源。不管切片在多高的位置,每个切片中正方形的面积与它的内切圆的面积之比是定值。这个比值为:
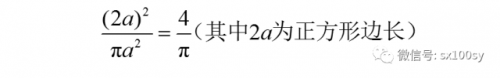
牟合方盖就是这样的正方形在垂直方向运动得到的,而那个内切的球是圆在垂直方向上运动形成的。所以,牟合方盖的体积与球的体积的比值就是4/π。于是便可以求出球的体积。
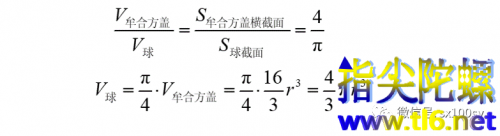
在外国,球的体积是很早就求出来的(阿基米德用一个有上下底面的圆柱体把球卡在里面不能动弹,则球的体积就是圆柱体积的三分之二,参见本公众号中《卡瓦列里原理 | 阿基米德对球体积的计算》一文)。