祖暅:解决牟合方盖问题的能言者
发布时间: 浏览: 次 作者:www.tl6.net

可惜刘徽未能求出牟合方盖的体积,他说:“欲陋形措意,惧失正理。
敢不阙([quē])疑,以俟(sì)能言者。
”意思是说,由于体积计算复杂,无奈只好留待有能之士图谋解决的方法。
(参见《刘徽-牟合方盖,完美助攻祖暅》)这一等啊,就从魏晋等到了南北朝,200多年之后,终于出现了一位“能言者”——祖暅。
祖暅出身名门,受父亲祖冲之的影响,从小热爱科学,对数学具有特别浓厚的兴趣。
祖暅从青年时代起,就为父亲的研究做助手。
父亲编《大明历》,他帮助观测;父亲推算圆周率,他协助摆弄算筹;父亲研制指南车,他准备材料。
后来,他就和父亲一起研究起刘徽的牟合方盖问题来。
祖暅意识到:牟合方盖虽然设计巧妙,但外形太复杂,不便于直接计算体积,必须另辟蹊径。
刘徽留下了2个极具价值的数学思想。
第一个就是牟合方盖本身的设计,它将球体体积问题转换成牟合方盖体积问题。
球体体积不好求,我们就来求牟合方盖的体积。
祖暅承袭了这种思想,既然牟合方盖的体积其实也并不好求,那就再设计一个可以求解的几何体。
刘徽留下的第二个数学思想——刘徽原理“同高的两个立体,在等高处各作一与底平行的截面,其截面面积之比为一常数,则此两立体体积之比也等于这一常数。
”祖暅则在刘徽原理的基础上,进一步发挥,提出了属于自己的祖暅原理:“缘幂势既同,则积不容异。
”就是:两个同高的立体,如果在任意等高处的截面积都相等,那么这两个立体的体积相等。
终于某一天,灵感来了。
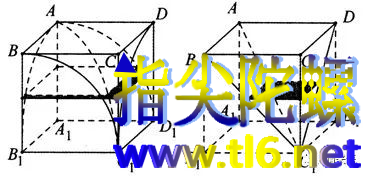
祖暅将牟合方盖一劈8份,在小牟合方盖外接了一个正方体。
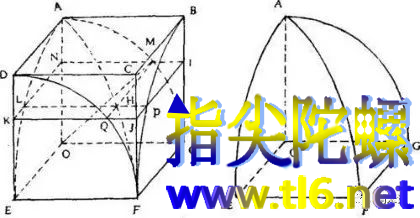
根据祖暅定理,其对应的体积也相等。
由于古人已经知道了正椎体的体积计算公式,因此也就能计算出牟合方盖的体积。
从而得到了正确的球体体积公式。