牟合方盖指的是什么?
牟合方盖
劳动出真知,这话一点也不假!很多人都没有见过实物的牟合方盖,哈哈,实话告诉你,铁匠师傅都知道!
冬天很冷啊,这不,小狗都受不了了!

上图小狗围着的叫做“火盆”,是北方过去取暖的一种方式,更多的是下面这张:

这叫“火炉”,请各位注意左侧烟道的拐弯处,那个结构就是牟合方盖,当然名字不是这个,叫“拐脖儿”。上世纪7,8十年代之前,会制作“拐脖儿“的师傅很多,估计现在很少了哦!
一道试题
这是某地区的一道高三数学模拟题:
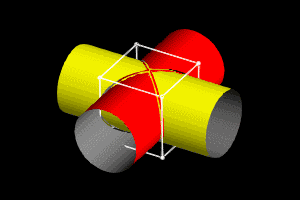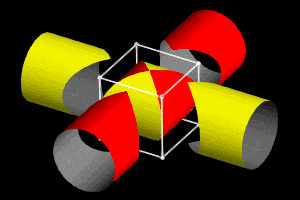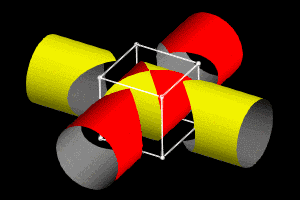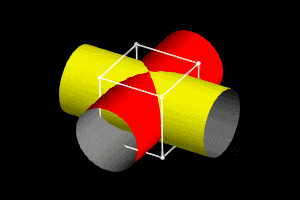
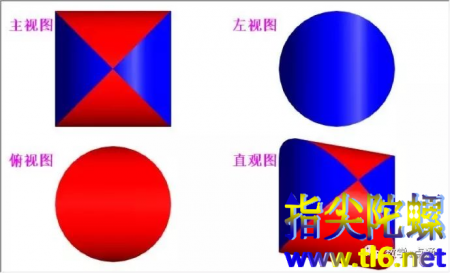
我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )
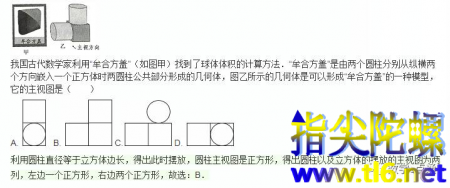
那么这个牟合方盖究竟应该怎么理解其中的数学知识?请各位继续往下看!
动图欣赏
这是牟合方盖的动图,可以从这里了解更多结构特征。


数学史料
是当一正立方体用圆规从纵横两侧面作内切圆柱体时,两圆柱体的公共部分。刘徽在他的注中对"牟合方盖"有以下的描述:"取立方棋八枚,皆令立方一寸,积之为立方二寸。规之为圆囷,径二寸,高二寸。又复横规之,则其形有似牟合方盖矣。八棋皆似阳马,圆然也。按合盖者,方率也。丸其中,即圆率也。"所谓“牟合方盖”,是以棱长为一寸的立方体八枚,合之则棱长为二寸的立方体。

又以过立方体中之二正圆柱垂直相贯并内切于立方体之相应侧面。则二内切于立方体的两垂直贯的正圆柱的共同部分,就叫“牟合方盖”。这是由于这个立体的外形似两把上下对称的正方形雨伞。
在这个立体里面,可以内切一个半径和原来圆柱体一样大小的球体。
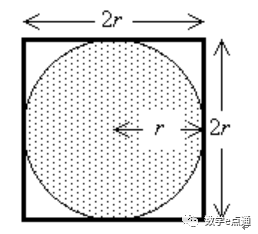
刘徽指出,由于内切圆的面积和外切正方形的面积之比为π:4(见图)所以球体体积与“牟合方盖”的体积之比亦应为π:4。
显然,只要求出牟合方盖的体积,那么球体积便迎刃而解。可惜的是,刘徽功亏一篑,未能求出牟合方盖的体积。
二百年后,能实现刘徽愿望的人终于出现了。他就是祖暅!祖暅是南北朝时代大数学家祖冲之的儿子。祖暅沿用了刘徽的思想,利用刘徽“牟合方盖”的理论去进行体积计算,他的方法是将原来的“牟合方盖”平均分为八份,取它的八分之一来研究。
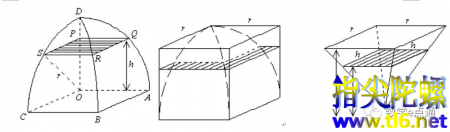
设OP=h,过P点作平面PQRS平行于OABC。又设内切球体的半径为r,则OS=OQ=r,由勾股定理,不难证明等高处阴影部分的面积总相等。所以,有理由相信,虽然方锥跟小正立方体去掉小“牟合方盖”后的形状不同,但因它们的体积都可以用截面面积和高度来计算,而在等高处的截面面积总是相等的,所以它们的体积也就不能不是相等的了。于是他提出了著名的原理:“缘幂势既同,则积不容异。”再根据刘徽的想法,可求出球体体积公式。