用笛沙格对合定理证明蝴蝶定理
今天我们用笛沙格对合定理来证明蝴蝶定理。这个证明方法简洁、有效。笛沙格对合定理是一个很难理解的定理,属于射影几何。我们今天给出这个定理,并对其进行一些说明,但不证明。然后,蝴蝶定理的证明反就极为简洁、有效。
笛沙格对合定理 一条直线截一条圆锥曲线于点对(S,S'),截圆锥曲线的内接四边形的三组对边分别于点对(A,A'),(B,B')及(C,C'),那么,这四个点对位于同一个对合中。

注:我们用同一大写字母(一个不带撇,一个带撇)表示点对,比如(A,A')。另外,上图中,四边形PQRT的三组对边分别是QR与PT,PR与QT,PQ与RT。
这个定理的结论“四个点对位于同一个对合中”可以理解为下面这些交比的等式都成立:
①(SABC)=(S'A'B'C')
上式中,左、右两边第i( i=1,2,3,4)个字母是点对。比如左边第2个字母是A,则右边第2个字母一定是A'。
②(SA′BC)=(S'AB'C')
即①中左、右同一位置的两个字母(点对的两个字母)可以互换(称可换的点对为共轭点对),即撇“'”可以在右边,也可以在左边。
③(SBCA)=(S'B'C'A')
即左边交比中字母顺序可以任意取,右边交比中的字母顺序跟着变化,只要保持左、右同一位置的字母是点对即可。(但交比中四个字母不能有重复。)
④由于四个点对都是共轭点对,所以(SBCB′)是允许的,所以有:
(SBCB′)=(S'B'C'B),
(SB′A'B)=(S'BAB′),
(C′A'CB)=(CAC'B′)。
说明:(a)直线上A、B、C、D四点交比的定义:
(ABCD)=(AC/BC)/(AD/BD)
(b)笛沙格对合定理需要我们努力去理解,虽然不是很容易。只从形式上去证明,读者仍然可能会不知所云。所以,我下面就要用这个著名的定理去证明另一个著名的定理。接下来的一期还要用它证明一个结论(与完全四边形有关,也与调合点列有关)。
下面用笛沙格对合定理来证蝴蝶定理。以前提及蝴蝶定理都是对圆来说的,所以用初等数学平面几何的方法也可以证。现在,我们在椭圆中进行。AA′为一条弦,C为AA′的中点。过中点C作两条弦DE和FG,其中D和F在弦AA′同侧。如图所示。再连接DG,连接FE。DG和FE分别与AA′交于点B和B'。我们要证明CB=CB′。
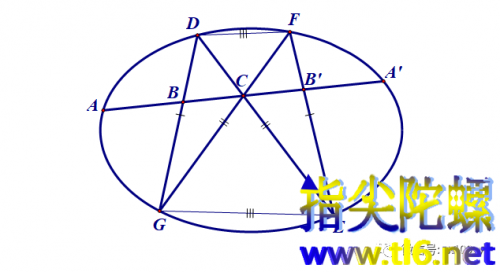
DGEF为对合定理中圆锥曲线的内接四边形。AA′为对合定理中与圆锥曲线和内接四边形相交的直线。于是,(A, A′)是一个共轭点对。DG与FE是内接四边形的一双对边,所以(B,B′)是一个共轭点对。DE与FG也是内接四边形的一双对边,它们的交点C既在DE上,也在FG上,所以(C,C)是第三个共轭点对(这时C与C′重合了)。对边DF与GE与直线AA′的交点在本题中我们可以不考虑。于是便写出某个交比等式,比如:
(ACBA′)=(A′CB′A)
即
(AB/CB)/(AA′/CA′)=(A′B′/CB′)/(A′A/CA)
因为CA′=CA,所以,
AB/CB = A′B′/CB′
两边都加1,得
AB/CB +1= A′B′/CB′ +1
即
(AB+CB)/CB =(A′B′+CB′)/CB′
AC/CB = A′C/CB′
CB = CB′
证毕。
