笛沙格对合定理与完全四边形
今天讲笛沙格对合定理与完全四边形的关系。很有意思!
(1)笛沙格对合定理 一条直线截圆锥曲线于点对(S,S'),截圆锥曲线的内接四边形的三组对边分别于点对(A,A'),(B,B')及(C,C'),那么,这四个点对位于同一个对合中。

注:我们用同一大写字母一个不带撇,一个带撇表示点对,比如(A,A')。另外,上图中,四边形PQRT的三组对边分别是QR与PT,PR与QT,PQ与RT。
(2)笛沙格对合定理中没有规定直线必须与四边形的内部边相交,所以,下图所示中的直线l,也是符合笛沙格对合定理条件的。只是四边形的外接圆锥曲线没有画出来,因为本题不需要。下图中,直线与四边形PQRS的三组对边QR与PS,PQ与RS,PR与QS分别交于点对(A,A'),(B,B'),(C,C')。
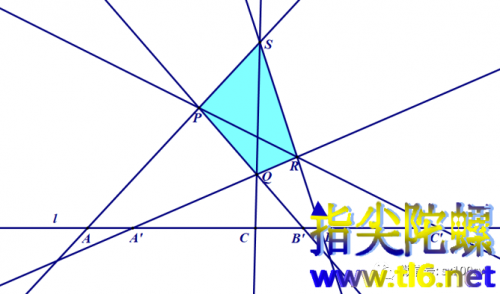
于是,有交比等式
(ABCC')=(A'B'C'C)
即
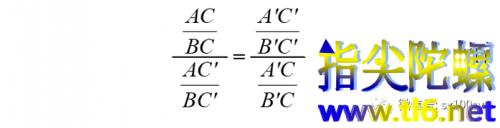
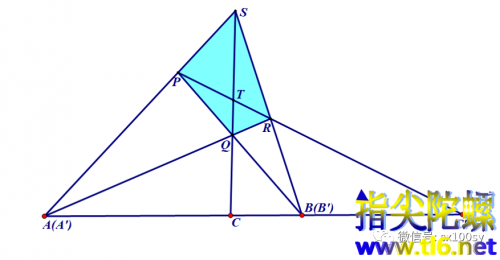
假定直线l移动到经过QR与PS的交点及PQ与RS的交点。这时,点A与A'重合,点B与B'也重合。得到完全四边形SPQRAB。如下图所示。
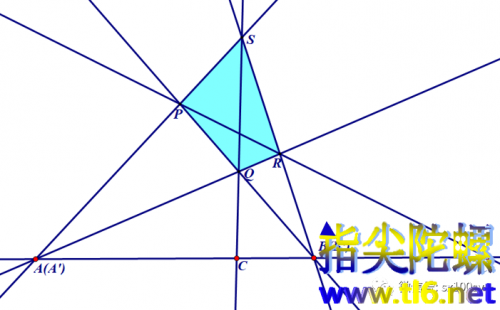
则(1)式变为
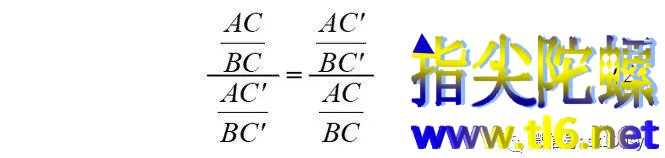
即
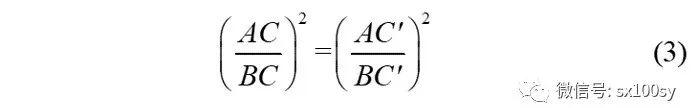
因为如图所示,对角线SQ一定与直线l交于线段AB之内,而对角线PR一定与直线l交于AB的延长线上。若不考虑线段的方向,即线段都是正的,则由(3)式有AC:BC=AC':BC',即点C和C'把AB调和分割。若考虑线段的方向,则AC:BC=-AC':BC',即(ABCC')=-1,这就是调和分割的交比定义。这就证明了有关完全四边形的一个定理中的一部分:完全四边形SRQRAB的对角线AB的两端被对角线SQ和PR调和分割。

(3)有关完全四边形的这个定理是说,完全四边形三条对角线中的每一条的两端,都被另外两条对角线调和分割。具体来说,如下图所示,(a)就是对角线PR的两端被对角线SQ和AB调和分割,即交比(PRTC')=-1。(b)对角线SQ被对角线PR和AB调和分割,即交比(SQTC)=-1。(c)对角线AB被对角线SQ和PR调和分割,即交比(ABCC')=-1(即这里用笛沙格对合定理所证的)。我们既然证明了交比(ABCC')=-1,那么,因为A、B、C、C′四点与P、R、T、C'四点关于点S是透视的(虽然SC′未画出),所以,交比(PRTC')=-1。再以点A为透视中心,则直线PC′上的点P对应直线SC上的点S;R对应Q,T对应T,C'对应C,所以,交比(SQTC)=(PRTC')=-1。
以上我们就用笛沙格对合定理简洁、有效地证明了完全四边形中有关调合分割的一个重要定理。利用这个调合分割关系,我们可以做一些有趣的事情。见下面的链接文章。
有关完全四边形的相关文章链接:
[1]完全四边形与藏宝图(2017-8-19)
[2]上一讲作切线方法的理论依据(2021-4-16)
[3]椭圆的共轭直径(2021-4-22)