笛沙格定理:十棵树排十行每行三棵怎么排?
有一个问题,不知是谁提出来的。这个问题是:要把十棵树栽种成十行,每行都有三棵树。问应该怎么栽种?
(0)在2016年1月5日讲过一个类似的问题,即要求种九棵树,这九棵树可以连接出十条线,每条线上都有不多不少三棵树。在那里,我是借此问题引出帕普斯定理的。具体内容详见文后的链接。今天所讲这个“十树排十行”问题则是与笛沙格定理有关。
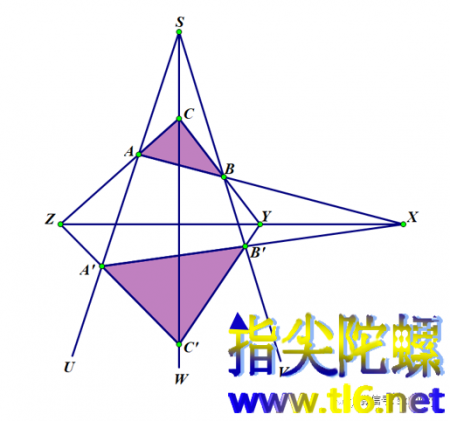
笛沙格定理我以前讲过很多次,这里先给出这个定理的结论:如上图所示,如果两个三角形ABC和A'B'C'对应顶点(A与A'、B与B'、C与C')的连线交于一点S,那么它们的对应边(AB与A'B',BC与B'C',CA与C'A')的交点(X、Y、Z)就位于一条直线(XYZ)上;逆定理也成立。

(1)让我们来数一数上图中一共有几个三条直线经过的点,几条过三个点的直线。这样的点(图中绿色)共有十个:A、B、C、A'、B'、C'、S、X、Y、Z。这样的直线也有十条:SAA'、SBB'、SCC'、XBA、XB'A'、XYZ、CBY、C'B'Y、CAZ、C'A'Z,它们都经过且只经过三个点,比如直线CBY所经过的点就是表示这条直线的字母C、B、Y。所以,我们只需在上图这样的十个点处种树,就可以做到把十棵树排成十行,每行不多不少有三棵树。栽树问题解决了,但数学知识并没有结束,我们一同来探讨。

(2)上图中的十个点都是彼此等价的。比如说,可以把上图中的点S当作射影中心,从它出发的三条直线分别经过三角形ABC和A'B'C'的对应顶点(A与A',B与B',C与C'),从而有三条对应边交点共线的结论,即笛沙格定理。其实,点X也有这样的功能:如下图所示,从点X发出的三条直线XBA、XB'A'、XYZ分别经过三角形BB'Y和AA'Z的对应顶点(B与A,B'与A',Y与Z),而这两个三角形的对应边(BB'与AA',B'Y与A'Z,YB与ZA)的交点(S、C'、C)当然共线(直线SCC'),即笛沙格定理仍然成立(射影中心为X)。
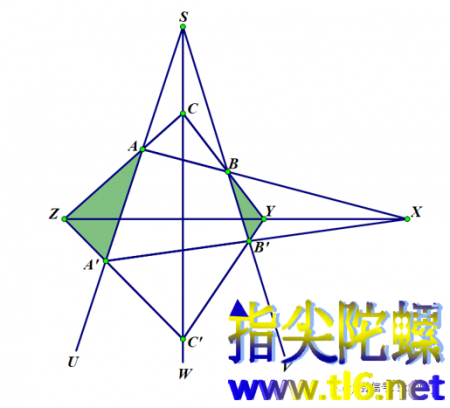
请您注意,我在上图中,已经把上上图中那两个涂以紫色的三角形去了色,而把这里所讨论的两个三角形BB'Y和AA'Z内部涂以另一种颜色(绿色)。后面我也是这样做的,这样看起来清楚明白。
(3)我们再换个中心。如下图所示,观察青色和蓝灰色的两个三角形ZAX和C'SB'(有部分重叠,不用管它)。一定要注意我写这两个三角形时三个字母的顺序,从这个顺序可以看出哪个顶点与哪个顶点是两个三角形的对应顶点,这里,点Z与C'对应,点A与S对应,点X与B'对应。那么,Z与C'的连线经过点A';A与S的连线也经过点A';X与B'的连线仍然经过点A'。即两个三角形ZAX和C'SB'对应顶点连线都经过点A',从而点A'是射影中心)。
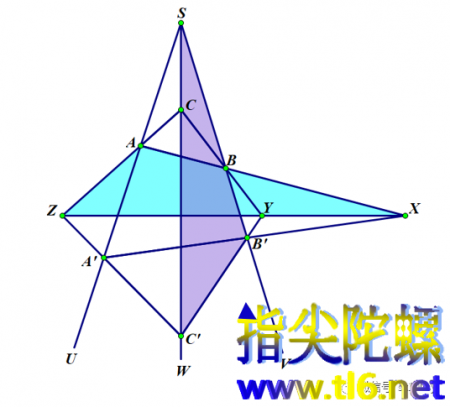
根据笛沙格定理,这两个三角形的对应边的交点应该共线。我们来看一看是不是这样:对应边ZA与C'S交于点C,对应边AX与SB'交于点B,对应边XZ与B'C'交于点Y,这三个交点C、B、Y确实在一条直线上(直线CBY)。
(4)我们再多举几个例子。比如以点C为射影中心,那么,这时从它发出的三条射线为CAZ、CBY、CSC'。于是,相关的两个三角形有可能是ABS和ZYC'。如下图所示。三对对应顶点(A与Z,B与Y,S与C')连线交于点C,三对对应边(AB与ZY,BS与YC'、SA与C'Z)分别交于三点(X、B'、A'),三点X、B'、A'共线(直线XB'A')。
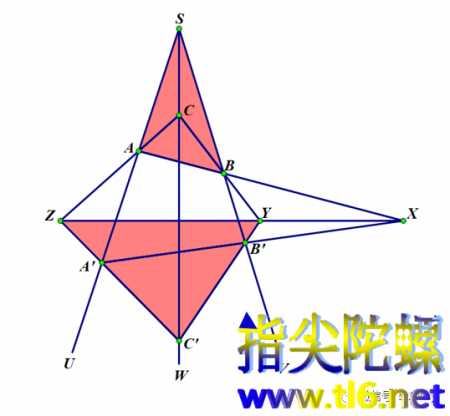
(5)若我们把类似上面给出的每一种情况都称为一种笛沙格构形,那么,由这十个点和十条直线组成的图形中,一共有多少种笛沙格构形呢?结论是120种(这里不具体讨论)。请您自己根据下图所示的这种笛沙格构形,找出射影中心是哪个点,射影直线是哪条直线?(对应顶点连线交于一点的两个三角形的三组对应边交点共线,这条所共之直线姑且称作射影直线。)(答案:A;YB'C'。)

(6)我们还可以更进一步。在上一图两个涂色三角形的基础上,再增加一个三角形BB'Y,如下图所示。我们来研究这三个三角形:①BSC,②BB'Y,③XA'Z。
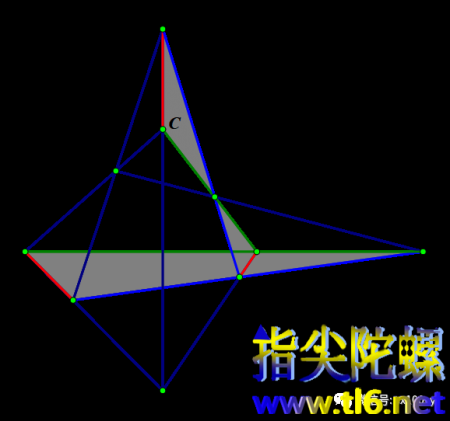
首先,①BSC与②BB'Y关于点B是透视的,我们把这两个三角形对应边用同一种颜色标出,不同的对应边标以不同的颜色,比如BS与BB'是对应边,都用蓝色标出,而BC与BY是另一组对应边,被标以绿色。其次,①BSC与③XA'Z是关于点A透视的,这个我们上一条研究过(B与X连线过A,S与A'连线过A,C与Z连线过A)。BS与XA'是对应边,也都标以蓝色,BC与XZ是另一组对应边,被标以绿色。

再来看②BB'Y与③XA'Z。点B与X对应,点B'与A'对应,点Y与Z对应,这三组对应点的连线交于点X,即两个三角形关于点X是透视的。好的,注意,我这里特意把三个射影中心的字母标以红色(B,A,X)。而这三个点正好就是某条直线上的三个点。这不是巧合吗。我们可以再来看另一个例子。
(7)可以再试一试下面这三个两两透视的三角形:①BSA,②BB'X,③YC'Z。首先,①BSA与②BB'X关于点B是透视的;其次,①BSA与③YC'Z关于点C是透视的;那么,②BB'X与③YC'Z的透视中心一定是直线CBY上除B和C外的第三个点Y。
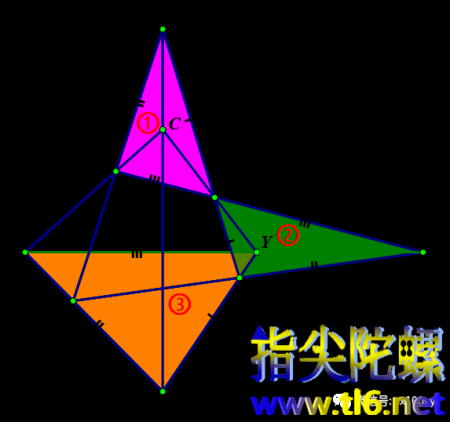
我们可以验证一下:②BB'X与③YC'Z的第一个字母B与Y的连线过点Y是吧;第二个字母B'与C'的连线也经过Y吧;第三个字母X与Z的连线还是经过Y。所以,这两个三角形的透视中心就是Y。
(8)还有一条不易发觉的性质,这里简单介绍一下。上图中三个三角形中每两个三角形三组对应边交点位于一条直线上,于是三个三角形两两组合,可以产生三条这样的直线,而这三条直线却是同一条直线。就以上图为例,①BSA与③YC'Z三组对应边(BS与YC',SA与C'Z,AB与ZY)的交点(B',A',X)位于直线XA'B'上。②BB'X和③YC'Z三组对应边(BB'与YC',B'X与C'Z,XB与ZY)的交点(B',A',X)位于直线XA'B'上。①BSA和②BB'X三组对应边交点连线也是直线XA'B'。
以上零零散散讲的这些仍然只是表面现象,要想把它们完全搞懂实属不易。我仍在研究的路上。谢谢阅读!
帕普斯定理:九棵树排成十行每行三棵怎么排?