在大刘的《三体》中，描绘了一个十维田园的年代，加上时刻，《三体》中的国际就是十一维度。

那么在数学中，怎么描绘这十一维的时空呢?

这个得说起咱们国家的一位大数学家--丘成桐，精确地说是美籍华人，由于他证明了数学上一个重要猜测--卡拉比猜测。

这个猜测的证明，得到了一个蜷缩的高维空间，6维度的卡拉比-丘成桐空间。

在1954年，意大利几何学家卡拉比，在国际数学家大会上，提出了一个猜测，内容是:在关闭的空间内，是否存在没有物质散布的引力场。

假如咱们看过其他数学猜测，应该有个形象，就是描绘越简略的往往最难证明，这个猜测就两句话，甚至连一个数学符号都见不到，证明起来可不简单。

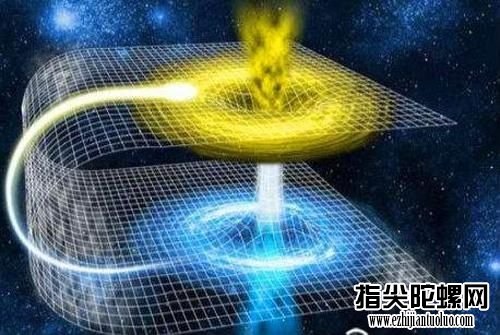
要了解这个猜测，咱们需求谈到爱因斯坦的广义相对论，广义相对论把时刻作为一个维度，加上咱们能了解的三维空间，一同组成了四维时空，这样的时空，咱们称作闵可夫斯基空间。

那么4维的闵可夫斯基空间，和蜷缩的6维卡拉比-丘成桐空间，就构成了咱们国际的十一个维度。

在闵可夫斯基空间中，时空是平整的，可是在去掉时刻维度后，三维空间就是不平整的，其曲率取决于空间中物质的质量，也就是相对论说的:物质通知空间怎么曲折，空间通知物质怎么运动。

而卡拉比猜测的空间，就不同于闵可夫斯基空间，这个猜测提出来后，简直没有人信任这样的空间存在，只要卡拉比自己信任是存在的，可是无法证明。

1970年，21岁的丘成桐正在美国加州大学念书，他对这个难题产生了爱好，历经2年的研讨，在1972年的一次重要会议上，丘成桐宣告他找到了卡拉比猜测的一个反例，并且台下的很多数学家，也觉得丘成桐的说法有道理。

两个月后，卡拉比给丘成桐来信，质疑他论说中一些观念，让丘成桐大吃一惊，由于他发现，他的论说中存在严峻的缝隙，不管他怎么补偿，都力不从心，终究不得不供认他的反例是过错。

然后丘成桐考虑，或许这个猜测是对的呢?然后他花了四年时刻，在1976年，证明了这个猜测，以此，丘成桐揽下了一切数学界的荣誉。

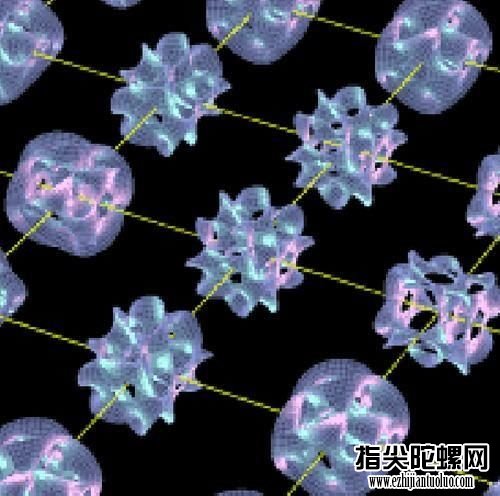
该猜测得到的空间，叫做卡拉比-丘成桐空间，该空间有6个维度，标准在普朗克间隔，相当于一个质子直径的万亿分之一，实在太小了，以至于现在没有任何试验手法能勘探，但它的存在，的确是合理的。

上图仍是计算机模仿的，一种类型的卡-丘空间在三维空间中的投影。

在超弦理论中，时空所需求的维度正好11个维度，所以说，咱们国际是4维的闵可夫斯基空间和6维卡拉比-丘成桐空间构成。