已知椭圆上的五个点,求作这个椭圆
五点可以决定一个椭圆。那么,在椭圆上任意选取五个点,把椭圆擦掉后,如何再根据这五个点作出这个椭圆呢?
前不久讲过如何过椭圆上一点作椭圆的切线(《过椭圆上一点作切线》,链接在文后),那里使用的是帕斯卡定理。今天的问题也是利用帕斯卡定理(有关帕斯卡定理的具体内容,可参见前些天的文章《对偶原理(帕斯卡定理与布里安香定理)》,链接在文后)。
帕斯卡定理一定是与椭圆内接六边形相联系的。
我们给已知的五个点按顺序起名1,2,3,4,5。我们的方法是找到运动的第6个点,让它的轨迹描出椭圆。依次作过点1和2,2和3,3和4,4和5的直线,得直线(1,2),(2,3),(3,4),(4,5)。如下图所示。(我们这里是用类似坐标的形式(x,y)表示过点x和y的直线。数学就是这样美妙,需要时,点的坐标的形式又可以用来表示直线。这不正巧应合了射影几何中点与直线对偶的性质。)
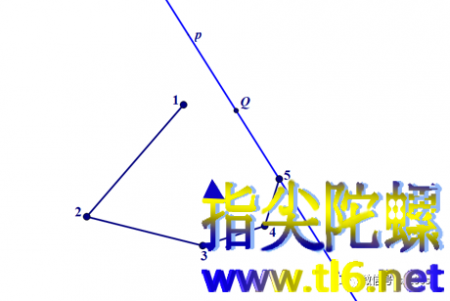
回顾一下帕斯卡定理,其中涉及了六边形的对边的概念。按照上面取点的顺序,我们的六边形是123456。其中边(1,2)和(4,5)是一对对边[另外两对对边分别是(2,3)和(5,6);(3,4)和(6,1)]。因为5个点是确定的,所以,(1,2)和(4,5)这组对边就是确定的。然后,过点5作一条可以绕点5转动的直线p(后面您会看到,正是因为在动,才可能产生轨迹)。但先固定直线p。如上图所示。因为直线p过点5,所以若假设椭圆已经作出,则直线p一定与椭圆交于两点,其中一点是5,另一个点就是6。但目前我们还不知道点6的具体位置,只知道它位于直线p上。即便如此,我们也已经知道了六边形123456的边(2,3)的对边一定位于直线p上。所以,我们就可以分别作出六边形123456两组对边及各一个交点。
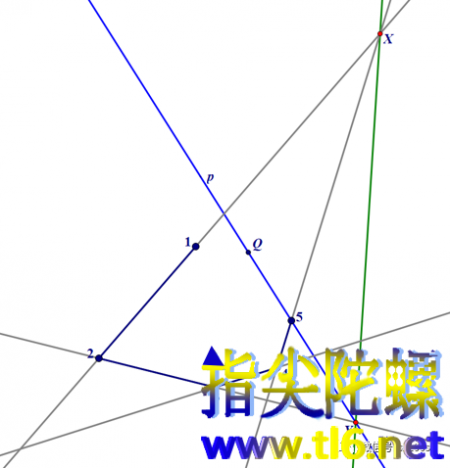
如上图所示。设对边(1,2)和(4,5)的交点为X;对边(2,3)和(5,6)所在直线p的交点为Y。两点确定一条直线,我们连接XY所在直线。虽然六边形还缺一个顶点6没有作出来,但这个六边形的帕斯卡线(帕斯卡定理中最后所说的三点共线之线)已经确定了。根据帕斯卡定理,第三组对边的交点一定位于这条帕斯卡线上。但是,第三组对边中有一条边即(3,4)是确定的,它与帕斯卡线一定有一交点,那么,我们就作出直线(3,4)与帕斯卡线的交点,设它为点Z。所以这个交点Z也就一定在(3,4)的对边所在直线上。(3,4)的对边是(6,1),而点1是确定的,所以,点1、6、Z位于同一条直线上。那么,我们连接点1和Z,得直线(1,Z)(下图中红色)。而点6又必须位于p上,所以,我们最终就确定出了点6,它就是直线(1,Z)与直线p(蓝色)的交点。如下图所示。
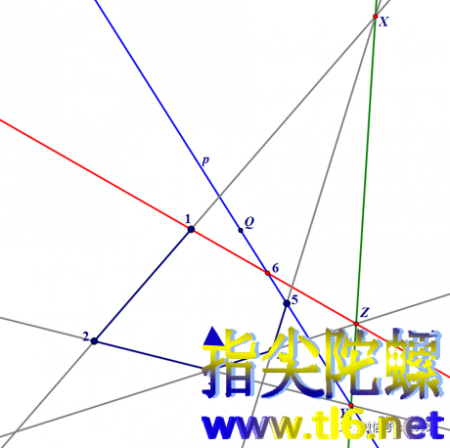
上图中,六边形123456就是椭圆的内接六边形。我们下面用动画展示点6的运动轨迹。可以让直线p绕点5转动。我们来看一看。
注意观察上面动画中,其中的蓝色直线是动直线。点6也在动,但它永远在动直线上动。这一动就画出了椭圆的轨迹。还要注意,我们的椭圆内接六边形是123456,必须是这个顺序,而不管点6移动到哪里。所以,这个六边形不一定是我们常见的凸六边形。
是不是很美妙,帕斯卡定理用好了,可以有很多有趣的变化。