椭圆的共轭直径的图解
发布时间: 浏览: 次 作者:www.tl6.net
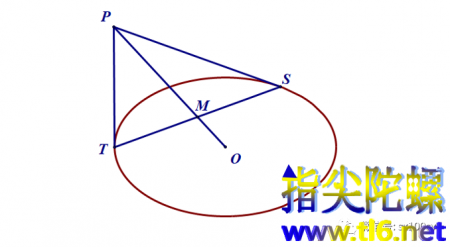
上两讲我们讲过从椭圆外一点作椭圆切线,还讲了把椭圆外这个点作为极点时,极点的极线是什么。极点到椭圆两条切线的切点的连线就是这条极线。比如下图中点P若为极点,则它的极线就是过切点S和T的直线。
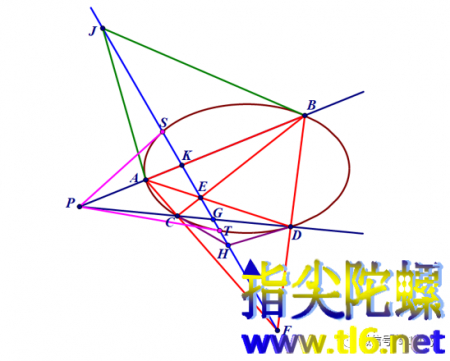
请问,极线什么时候通过椭圆中心?
可以看出,若点P离椭圆越来越远,则两条切线就越来越平行。当点P到达无穷远时,两条切线就平行了(或者说,平行线的交点在无穷远)。这时的两个切点就是椭圆的“对径点”,即两切点连线是椭圆的一条直线,即经过椭圆中心。以上是直观的考察。我们也可以通过完全四边形来加以说明。

上图中,若P到达无穷远点Q,则由(BA|KQ)=-1,得
(BK/AK):(BQ/AQ)=-1
但是,因为Q在无穷远,所以BQ=AQ。从而
BK/AK=-1
即
BK=-AK
这说明点K一定位于BA的中点。同理点G位于CD中点。

并且AB平行于CD。从而无穷远点Q的极线GK就是过椭圆中心的直线。也可以说,无穷远极点的极线位于椭圆内部的线段,是从无穷远极点向椭圆所引割线位于椭圆内部线段的中点的轨迹。

过无穷远点Q引过椭圆中心的割线之位于椭圆内部的线段与点Q的极线位于椭圆内部的线段都是椭圆的直径。椭圆的直径有无数多条,而只有像上面这样作出的两条直径才有特殊的关系,我们叫它们为共轭直径。共轭直径就是与一条直径平行的弦中点的轨迹。
所以,如果过椭圆外一点作椭圆的两条切线PS和PT,则ST就是切点弦;再连接点P与椭圆中心O,得线段PO。那么PO与ST的交点M平分切点弦ST,即SM=MT。如下图所示。