圆周率是谁发明的?圆周率是什么?圆周率怎么算?
发布时间: 浏览: 次 作者:www.tl6.net

数学系没有白色情人节
又到了一年一度的白色情人节圆周率日。

每年的3月14日,π爱好者们都会举行各种集会,一起讨论有关π的话题,举办各类活动以庆祝“π日”。
超模君也心痒痒想搞个什么活动,比如模友答对一个问题,就送一个小天亲手做的派
 。
。

不过,后来想想,小天的手艺经常有时刹不住手,一不小心就会做出诸如下面这种黑暗料理。

很有shǐ的feel
为了防止模友被小天做的派恶心到,超模君决定自己动手了,精心准备了一顿名为“关于π你所不知道的N个事实”的大餐,下面各位模友可以尽情享用啦!
关于π的起源
现在的我们都知道圆的周长与直径之比是π≈3.14,知道它是一个无理数,也是一个超越数。
其实,人们对π的理解经历了一个漫长的过程。
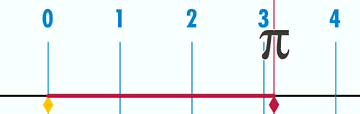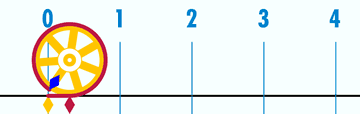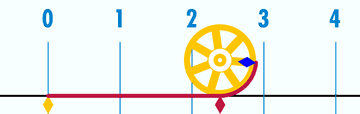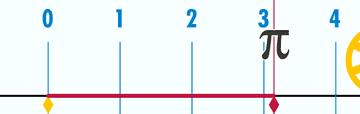
圆周率自诞生伊始,便与人类“纠缠”了近4000年。
而π,在希腊字母中排行第16位,是希腊语περιφρεια(边界、圆周之意)的首字母。
尽管在四大古文明里早就有它的身影,但是,π真正作为一个通用常数被重新定义,也不过是近300年的事情。
据史料记载,1631年,π首次出现在数学家威廉奥特瑞德的著作《数学之钥》中;1706年,英国数学家威廉琼斯在他编写的数学教材《新数学导论》里也提到了π。
不过,此时的π估计还是欠些火候,并没有引起数学界太大的关注,直至遇到欧拉。

(点击图片,开启你的数学之旅)1748年,欧拉的代表作《无穷小分析引论》出版,在这本著作里,欧拉建议用符号“π”来表示圆周率,并且直接在里面使用了π。
在欧拉的积极倡导下,π终于成为了圆周率的代名词。

关于π节的来历
接着,π以它自身的“才华”,非常机灵地植入到各种公式里,就连最美公式“欧拉恒等式”也看到它的身影。
作为一个常数,也许是由于π的定义极其简单且在数学公式里随处可见,π在流行文化中出现的频率可以说是狂甩其他常数一条街。
自然而然,π节就这样诞生了。
(其他常数只能两眼泪汪汪)超模君了解到,最早的一次以π为主题的大型庆祝活动是美国旧金山科学博物馆的一位物理学家LarryShaw组织的。
在1988年3月14日那天,LarryShaw带着博物馆的员工以及其他参与者,一起绕着博物馆的纪念碑转了22/7(π的近似值)圈,还一起吃水果派、分享与π有关的知识。

此后,每一年的3月14日,旧金山科学博物馆都会举办π的庆祝活动。
后来,越来越多热爱数学的人留意到这个特殊的日子,也越来越多的人参与到π节的活动上来。
不过,大家节过多了,肯定也希望能够帮自己过的节拿个名分,麻省理工学院首先发起了将3月14日定为“国际圆周率日”的倡议。
到2009年3月11日,美国众议院终于正式通过一项无约束力决议,将每年的3月14日定为“πday”。
然后3141年5月9日(2时6分5秒)就是“终极圆周率日”。

对π的情结
在2010年的圆周率日,谷歌推出了π的GoogleDoodle,图中包含了π的定义、π值范围、圆周长公式与圆面积公式、圆内切以及外切多边形、球体积公式、圆柱体积公式。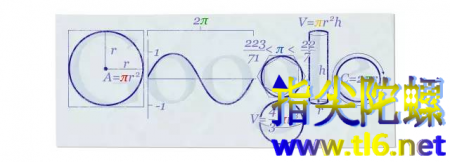
2010年3月14日的GoogleDoodle其实,这不是谷歌第一次如此“贴心”了,早在2005年谷歌的第一次公开募股中,总共集资40多亿美元,A股的发行量是14159265股,这股数就是从π的小数点后的位数得来的。
而著名的排版系统TeX的版本号码也是十分有趣。
自第三版开始,之后的升级都是在小数点后加入一位新的小数,使得它越来越接近π的值,比如,版本3.1,版本3.14,版本3.141……TeX目前的版本是3.1415926,这说明了TeX系统已经非常稳定,每一次的升级都只是弥补一下那些极小的漏洞。
其发明者——著名的计算机科学家高德纳(DonaldE.Knuth)就曾表示“(在我过世后的)绝对最后改变’为把版本数改为π,那时任何余下的漏洞都成程序的点缀了。
”

高德纳对π的情结,不仅仅是理工男的专属,文学家也抵挡不住π的诱惑,一不小心就独创了一个新的文体——“π体”。
比如迈克·基斯(MikeKeith)所写的诗《CadaeicCadenza》,开头就是:One/Apoem/Araven,每个单词的字母数就是3、1、4、1、5,刚好与π的近似值3.1415符合,全诗近4000个单词,都是这样的形式写的。

可以说是非常合格的π迷了说到π迷,这又让超模君想起了日本的“暗黑通信团”,这是由一群疯狂的理工男组成的神秘组织,这个组织经常出版一些看起来非常牛逼并且书名更加牛逼然而可能并没有什么卵用的书籍,比如《素数15万个》、《自然数e100万位》、《无限级数集》等等。

作为一群正经的π迷,暗黑通信团对待π当然也是特别的,直接来了个连载杂志《月刊圆周率》,每个月10万位的π。

为了方便阅读,暗黑通信团在书的开头就写明了数字的排列方式,每页限定10000位,每行限定100位,即是说,倘若你要找π后面的第12345位,那么就需要翻到第2页,然后去第24行找就对了。


也许我你会觉得,这本书简直无聊至极,但是,你不可否认,这本书作为随机数表的用处,你随便翻开一页,然后拿铅笔随便一戳,戳到哪个数字就是哪个数字,简直随机到不能再随机了!ps顺便提一句,这个社团的画风确实配得起他们名字的:

这是巧合吗?
关于3.14,还有一个令人兴奋的事实:爱因斯坦的生日也是这一天。
由于爱因斯坦在普林斯顿生活了很长一段时间,因此,在每年的3月14日,普林斯顿都会举办很多活动,同时庆祝圆周率日兼爱因斯坦生辰。
除了常规的吃派活动,以及π值背诵比赛之外,在这一天,还有一个爱因斯坦cosplay比赛。
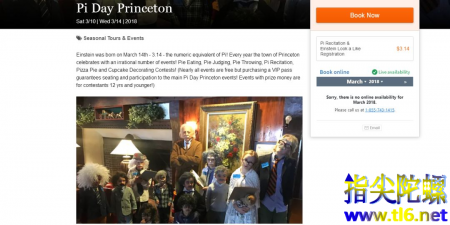
截自普林斯顿πday网站关于3.14,还有另一个令人意外的事实:最接近宇宙的男人--霍金去世也是在这一天。
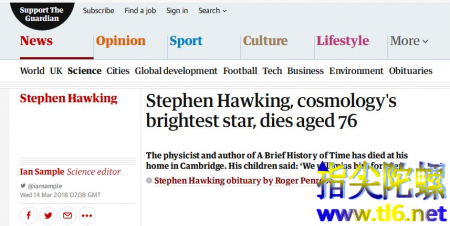
霍金的离去,似乎又再一次提醒世人,记住这个特殊的日子。
π决定了河流的曲折程度?相信大部分模友都听说过这个说法:地球上所有河流的长度都大致等于从起点到终点直线距离的π倍。
人们统计过的河流越多,平均值就越接近π。关于这个说法,超模君之前已经作过论证(传送门),现实中并没有这样的河流。
π的平方与重力加速度g在数值上极其接近。
哇,这就神奇了,吓得小天赶紧拿计算器算了一下,3.14159²=9.8695877,与g=9.81m/s²还真的就差一点呢。
看到这里,也许有人就会跳出来说,各星球重力加速度不同、量纲不同,这一看就是巧合啊。
其实,这个巧合是历史上第一个关于“米”的定义导致的。
在1688年,英国人威尔金斯建议用钟摆的方法来确定标准长度。
然后,在1790年,法国国民议会将“米”定义为:“纬度45度的海平面上半周期为1秒的单摆的摆长”。
那么,根据单摆的周期公式
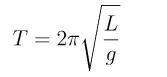
T=2秒,L=1米,就立刻能够得出g=π²m/s²。
当然,如今的“米”就不是之前的那个“米”了,如今的“米”是指光在真空中1/299792458秒时间间隔内行程的长度。
关于π是否包含了所有可能的数字组合,这个超模君只能回答:看你怎么想的咯。

圆周长与直径之比,无穷无尽,永不重复。
在这串数字中,包含每种可能的组合。
你的生日、储物柜密码、社保号码,都在其中某处。
如果把这些数字转换为字母,就能得到所有的单词,无数种组合。
你婴儿时发出的第一个音节,你心上人的名字,你一辈子从始至终的故事,我们做过或说过的每件事,宇宙中所有无限的可能,都在这个简单的圆中。
用这些信息做什么,它有什么用,取决于你们。
最后,就再来一首歌,让各位再感受一下π的无穷无尽吧。