梅森数及梅森素数
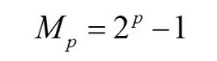
的数叫做梅森数,其中p为素数。
为什么这个定义中要求p是素数?若p不取素数而取合数,那么,2的合数次方一定是一个完全平方数,那么根据平方差公式,2的合数次方再减1,就一定可以分解成两个正整数的乘积。也就是说,2的p次方再减1这种形式的数在p为合数时,一定是合数。于是,结果是合数,研究的价值就少了很多。
但是,就算梅森数的定义中要求p是素数,也不能保证梅森数一定是素数。梅森数可能是素数,也可能不是素数即合数。我们列出p取前面一些素数时的梅森数,并指出它们是素数还是合数。

从上表看,好象素数多于合数。其实不然。上表若再往后列出,素数的情况就远少于不是素数的情况。目前已经证明了,梅森素数的个数是无穷多的。而梅森数列变大的速度非常之快,所以,通过梅森数,数学家们可以更加容易地发现更大的素数。
因为梅森素数很快就变得很大很大,并且后一个梅森素数比前一个梅森素数要大上很多很多,所以,稍微大一点的梅森素数动辄就有几十位、几百位甚至几千位,......。今天我就讲一讲梅森素数位数的计算。(其实就是梅森数的位数的计算。)
以p取152为例。已经证实,p=521时的梅森数是素数:

它是一个具有157位的正整数,这已经是一个很大的数了。但因为素数有无穷多,所以,这个157位的素数也真的不算大,或者说很小。一般来说,我们常用的计算器是显示不出完整的157位的这个梅森素数的。其实我们也没有必要写出这个157位的素数来。但是,这个157位数的“157”,是怎么知道的呢?算出一个梅森素数有多少位,倒是一个很有趣的事情。这并不难办到。我们下面就来算一算M521这个梅森素数的位数。
首先,我们要说明,梅森素数

与它的下一个正整数(即比它大1的正整数)

具有相同的位数。因为若不具有相同位数,而后者又比前者大1,那么,前者就一定是以0结尾的正整数。但是,2的正整数次方都是以2,4,6或8结尾的,所以,梅森数M521是以1,3,5或7结尾的,不可能以0结尾。也就是说,梅森素数M521加1后,不足以增加位数。于是,我们要计算梅森素数M521的的位数,只需计算2^521的位数就可以了。
给“2的521次方”取以10为底的对数,得到
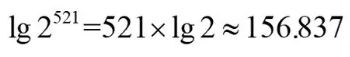
把对数式转换成指数式,得到

“10的156次方”是一个具有157位数字的正整数,并且是所有具有157位数字的整数中最小的一个:
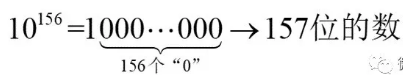
“10的157次方”是一个具有158位数字的正整数,并且是所有具有158位数字的整数中最小的一个:
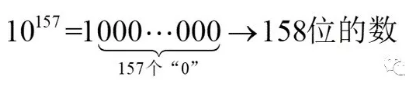
由于
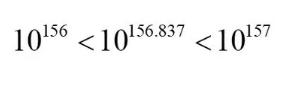
所以,

好的,今天就讲到这里,下期讲一讲梅森数与完全数的关系。敬请关注和阅读。