“定和幂圆”与三角形作图
今天给出一个重要结论,然后利用这个结论解一道三角形作图题。其中用到之前不远的某期讲过的代数解析法。
我们知道,如果一动点到一条定线段两个端点的距离的平方和等于这条定线段长度的平方,那么这样的动点运动的轨迹明显是一个圆(根据勾股定理的逆定理)。
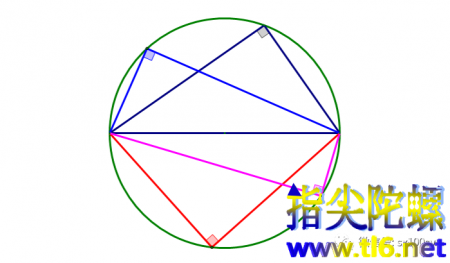
仍然是这一线段,但是如果动点到它的两个端点距离的平方和不等于这条线段长度的平方,而是等于另一数k的平方,那么这时动点的运动轨迹是什么曲线呢?
我们知道,平行四边形四条边的平方和等于两条对角线的平方和,即
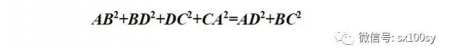
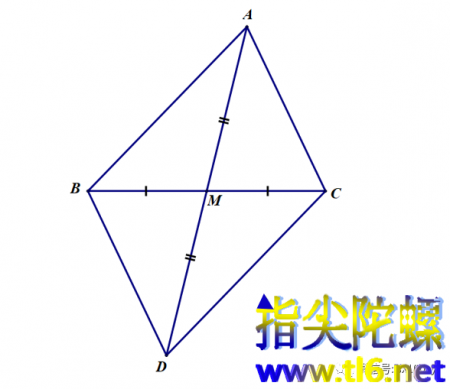
因为AB=DC,BD=CA,又因为AD=2AM,所以上式变为
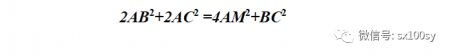
两边同时除以2,得三角形ABC中三边与一边上中线的关系:
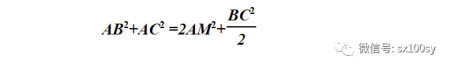
即,三角形两边的平方和等于第三边的平方的二分之一加上第三边上中线平方的二倍。
考虑到本问题中动点与两个定点正好构成一个三角形,所以,不妨让动点为A,两定点为B和C。于是,根据问题条件,就有动点A到两定点B和C的距离的平方和等于定值,即
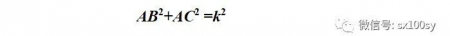
再设定点B和C所连线段中点为M(当然也为定点),B和C之间的距离为a,那么,就可以求出动点A到M的距离:
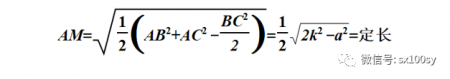
这个变化的AM的长度是一个定值。这说明不管动点A怎么动,它到BC中点M的距离都是定长,所以动点的轨迹是一个以两定点连线中点M为圆心且以定长为半径的圆。
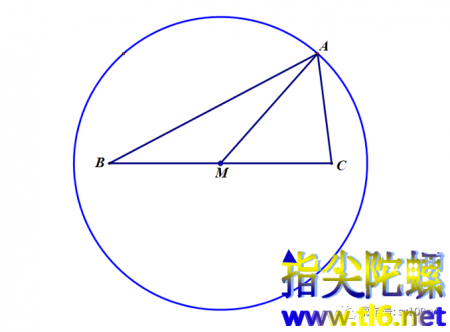
于是我们便得到下面这个结论:到两个定点距离的平方和等于某数k的平方的点的轨迹是一个以两定点连线中点为圆心以“k的平方的2倍与a的平方的差的开平方再除以2”为半径的圆,其中a为两定点之间的距离。这个圆叫做定和幂圆。所谓“定和幂”是指到两个定点的幂的和是定值,有这种性质的点的轨迹是一个圆。
这个半径是由已知的k和a经过有限次有理运算及开平方运算得到的,所以,可以用尺规作图作出。但要注意,因为有开平方运算,所以,平方根下的值应该大于0。这就要求k的根号2倍要大于a。
下面用这个结论来完成一个三角形作图题。
第18题:已知三角形一边a,这边的对角∠A,另外两条边的平方和等于k的平方,求作三角形ABC。
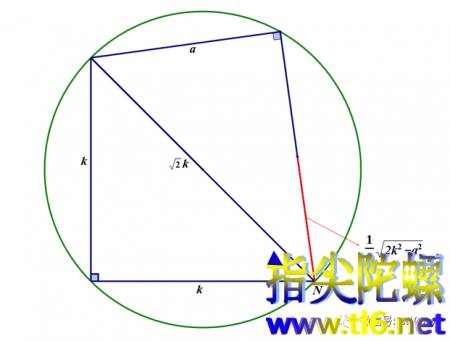
先作出长度为a的边BC,再以BC为弦作内接角为定角∠A的弓形弧BA'C。所求作的三角形的第三个顶点A一定位于这个弓形弧上(这是点A所在的第一条轨迹)。下面还缺少另一个条件来确定点A。我们还有b^2+c^2=k^2这一条件没用上。明显地可以应用刚才得到的结论。也就是说,点A还应该位于以BC中点M为圆心,以“k平方的2倍与a的平方的差的开平方的二分之一”为半径的圆上。所以需要作出这个圆。半径“k平方的2倍与a的平方的差的开平方的二分之一”是可以作出的。作法如下图所示:
如下图所示,第一条轨迹——绿色弓形弧与第二条轨迹——蓝色定和幂圆的交点,就是所要求作的三角形ABC的顶点A。再连接AB,AC,就得到满足所给条件的三角形ABC。
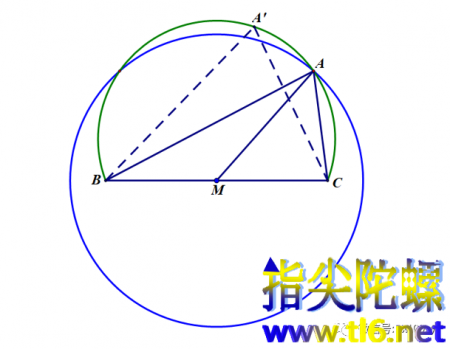
注意,k的取值不仅要使得可以作出“定和幂圆”,还要使得作出的定和幂圆与弓形弧有交点,这样才能作出三角形。这里不再给出,请您自己研究一下吧。