神奇的缺8数和走马灯数
发布时间: 浏览: 次 作者:www.tl6.net
今天小编给大家介绍数学中最最神奇的两组数字——缺8数和走马灯数,一起感受数学的神秘力量
。
1.缺8数——12345679(1)“清一色”哈哈,这个可不是打麻将时候的清一色,而是缺8数的一种神奇形式。
规律是缺8数与1—81中9的倍数(9,18,27,36,45,54,63等)相乘可以得到一串“清一色”的数字。

(2)“三位一体”当缺8数与3,6,12,15等3的倍数但不是9的倍数的数字(3、6、12、15、21等)相乘时,会得到三位一体的数字:

其中也有特殊情况,如12345679×345=4259259 255,这同样是缺8数,结果的首位数4加到尾数上,即255+4=259,此时也是符合缺8数的“三位一体”形式;再如12345679×1245=15370370 355,首二位数15加到尾两位数上,355+15=370,也符合缺8数“三位一体”的形式。
(3)“轮流休息”当缺8数与不是9或3的倍数(10、11、13、14、16、17等)相乘时,此时虽然没有“清一色”或“三位一体”的现象,但仍可以看到一种“轮流休息”的性质:乘积中的各位数字均无雷同,并总是缺少1位数字。

另外,乘积中缺3、缺6、缺9的情况肯定不存在,就轮不到它们休息了~ (4)走马灯之谜当缺8数与形如等差数列9n+1的数(10、19、28、37、46等)相乘时,会使1、2、3、4、5、6、7、9这8个数字不断轮换顺序,如同走马灯一样:

当我们竖着看的时候,可以很清楚地看到规律:123456,234567,345679,456790……进一步挖掘可知,走马灯之谜可以由“清一色”推断出,属于“清一色”的一个变数。
总数在“清一色”(9的倍数)的基础上加一个缺8数(9n+1)。

以上就是缺8数的介绍,是不是很神奇?

传言缺8数还有一个小故事:菲律宾前总统马科斯偏好的数字是7(既不是六六大顺的6、也不是恭喜发财的8)。
于是有人对他说:“总统先生,你不是挺喜欢7吗?拿出你的计算器,我可以送你清一色的7。
”
接着,这人就用“缺8数”乘以63,顿时,777777777映入了马科斯先生的眼帘。

2.走马灯数-142857据说走马灯数142857最早被发现于埃及的金字塔内,可以证明一星期有7天,被称为世界上最神奇的数字,它神奇在哪里呢?(1)走马灯142857的1~6倍都是1、4、2、8、5、7这几个数字的重新排列,只是每次数字的顺序略微调整了一下下。

这类似于一周7天,前6天每天都由1、4、2、8、4、7以不同的排序出来站岗,但我们不禁要问了,第7天怎么办呢?让我们一起来看一看。
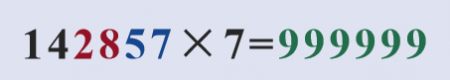
原来啊,第7天的时候之前的数字1、4、2、8、4、7全都放周假了,由999999这个幕后大boss出来站岗。
(2)“分身术”以142847×8=1142856为例,1142856的首位数字1和末位数字6是由原走马灯数中的7分解而成,所以被成为7分身。

同样的"分身数"规律,142857的8~14倍如下:

除了上述“走马灯”和“分身数”规律,走马灯数还具有这样的神奇特性。
单位数相加、双位数相加、三位数相加以及乘以7都可以得到全为9的数字。

以上就是今天关于缺8数和走马数的介绍,你还知道哪些奇奇怪怪的神奇数字?
。
1.缺8数——12345679(1)“清一色”哈哈,这个可不是打麻将时候的清一色,而是缺8数的一种神奇形式。
规律是缺8数与1—81中9的倍数(9,18,27,36,45,54,63等)相乘可以得到一串“清一色”的数字。

(2)“三位一体”当缺8数与3,6,12,15等3的倍数但不是9的倍数的数字(3、6、12、15、21等)相乘时,会得到三位一体的数字:

其中也有特殊情况,如12345679×345=4259259 255,这同样是缺8数,结果的首位数4加到尾数上,即255+4=259,此时也是符合缺8数的“三位一体”形式;再如12345679×1245=15370370 355,首二位数15加到尾两位数上,355+15=370,也符合缺8数“三位一体”的形式。
(3)“轮流休息”当缺8数与不是9或3的倍数(10、11、13、14、16、17等)相乘时,此时虽然没有“清一色”或“三位一体”的现象,但仍可以看到一种“轮流休息”的性质:乘积中的各位数字均无雷同,并总是缺少1位数字。

另外,乘积中缺3、缺6、缺9的情况肯定不存在,就轮不到它们休息了~ (4)走马灯之谜当缺8数与形如等差数列9n+1的数(10、19、28、37、46等)相乘时,会使1、2、3、4、5、6、7、9这8个数字不断轮换顺序,如同走马灯一样:

当我们竖着看的时候,可以很清楚地看到规律:123456,234567,345679,456790……进一步挖掘可知,走马灯之谜可以由“清一色”推断出,属于“清一色”的一个变数。
总数在“清一色”(9的倍数)的基础上加一个缺8数(9n+1)。

以上就是缺8数的介绍,是不是很神奇?

传言缺8数还有一个小故事:菲律宾前总统马科斯偏好的数字是7(既不是六六大顺的6、也不是恭喜发财的8)。
于是有人对他说:“总统先生,你不是挺喜欢7吗?拿出你的计算器,我可以送你清一色的7。
”

接着,这人就用“缺8数”乘以63,顿时,777777777映入了马科斯先生的眼帘。

2.走马灯数-142857据说走马灯数142857最早被发现于埃及的金字塔内,可以证明一星期有7天,被称为世界上最神奇的数字,它神奇在哪里呢?(1)走马灯142857的1~6倍都是1、4、2、8、5、7这几个数字的重新排列,只是每次数字的顺序略微调整了一下下。

这类似于一周7天,前6天每天都由1、4、2、8、4、7以不同的排序出来站岗,但我们不禁要问了,第7天怎么办呢?让我们一起来看一看。
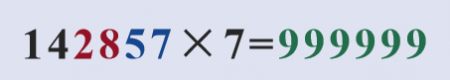
原来啊,第7天的时候之前的数字1、4、2、8、4、7全都放周假了,由999999这个幕后大boss出来站岗。
(2)“分身术”以142847×8=1142856为例,1142856的首位数字1和末位数字6是由原走马灯数中的7分解而成,所以被成为7分身。

同样的"分身数"规律,142857的8~14倍如下:

除了上述“走马灯”和“分身数”规律,走马灯数还具有这样的神奇特性。
单位数相加、双位数相加、三位数相加以及乘以7都可以得到全为9的数字。

以上就是今天关于缺8数和走马数的介绍,你还知道哪些奇奇怪怪的神奇数字?