阿波罗尼圆法:两点被另外两点调合分割的方法
发布时间: 浏览: 次 作者:www.tl6.net
第4种方法:阿波罗尼圆法
点A和B被点C和D调和分割,设点C已知,它位于线段AB之上,且不妨设点C与点B较近。我们要求点D,使得AC:BC=AD:BD。所谓阿波罗尼圆,就是指到两个定点距离的比值为常数k的点的轨迹。显然,阿波罗尼圆与直线AB的两个交点一定把AB调和分割。现在,点C已知,则比值AC:BC就是确定的了,即AC:BC=k。所以,我们只要作出到点A和B的距离的比值为AC:BC的阿波罗尼圆即可。(有关数学家阿波罗尼,可自行搜索。)
作法很简单。2018年8月5日的文章《轨迹题系列(之一)——阿波罗尼圆》讲过,可以文后点链接跳转到那篇文章。
本期讲用最基本的方法——比例法作阿波罗尼圆。
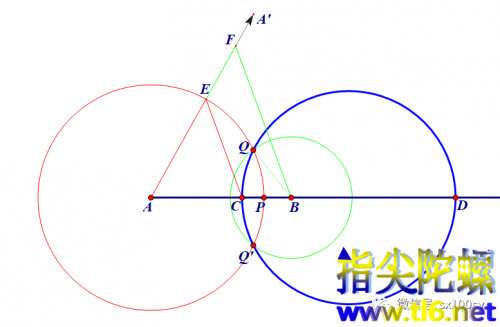

我们以点A为顶点作射线AA',与射线AB有一个夹角。在AA'上取AE=AP。连接CE。过点B作CE的平行线,与AA'交于点F。则三角形ACE相似于三角形ABF。那么,AC:CB=AE:EF=k,即都是已知的比例k。那么分别以点A和B为圆心,以AE和EF为半径作圆,则两圆的交点Q或Q'就是阿波罗尼圆上的一点。随着点P在射线CB上的运动,点Q就描绘出阿波罗尼圆。设这个圆与直线AB的交点为D。所以一定有AC:CB=AD:DB,所以点D就是第二个调和分割点。