无限猴子定理的无限之美
研究概率论的大师们也尤其喜欢拿“无限”开涮,在无所限制的命题世界里,他们拥有了无限的时间和无限的资源,所以他们可以尽情发挥自己天才头脑的能力,然后写出一些让普通人看了后脑袋爆炸的理论。

就像民科中曾有一个说法:地球形成的概率是10亿亿分之一,大约相当于在标准游泳池水面上漂浮着一个闹钟的全部零件,它们随着水流组装在一起的概率。没人知道这个概率是怎么算出来的,也没有人可以证明其对错,别管科不科学,这听上去十分浪漫不是吗,你与我们,人类的诞生就是这样一个奇迹。
E·波莱尔先生加入了这“无限之美”的行列,他在撰写的概率论图书中提出了这样一个理论:“无限猴子”。

这个理论有一个直白的名字,其内容解释起来也通俗易懂:波莱尔拥有了无限的时间,百无聊赖之中,他雇佣了一只猴子,把猴子抓到一台新买的打字机面前,让猴子打字,可是猴子并不识字,于是它就在打字机上乱摁一气,打出一页又一页的乱码。此时波莱尔已经拥有了无限的时间和纸墨,便任由这只猴子肆意“挥洒才华”,终于,在经过了不知多久的时间之后,也许是无限秒之后,这只猴子靠着一顿乱摁打出了完整的莎士比亚全集,一字不差。

这听上去有点像强化版的愚公移山,子子孙孙无穷尽也,终有一日再高的山峰也会被填平,只要有了无限的时间,在岁月长河里,靠着各种事件的随机组合,最后竟然都可以通向一个正确的答案。

一切看似是机缘巧合,但又有一种命中注定的味道。
这听起来不像是科学,因为显示不存在恒定不变的实验条件,我们甚至都不知道时间这一概念是不是无限的。似乎简单的一句“万事皆有可能”就涵盖了所有的有关无限的概率理论。但是我们今天显然不是来给大家讲人生大道理的,这个有趣定理背后还有一个更有趣的故事。

一个科学定理和一个民间推论最大的区分方法就是看它们能否被科学的实验所证实,我们显然无法进行无限猴子的实验,我们没有一只任劳任怨不停打字的猴子,也没有墨水无限的打字机,更没有那闲功夫去等待猴子完成它的著作。
疯狂的理论需要由疯狂的人员去验证,有位年轻人巧妙地做了一个类似无限猴子的实验,能完成一个看似不可能的任务,听上去就让人很兴奋,就像是目睹了愚公在有生之年把山移走那样让人激动。

我们先来回味一下童年的乐趣——口袋妖怪,口袋妖怪是笔者最喜欢的掌机游戏,它的操作虽然简单,但是控制里面的角色踏上旅程,收服Pokemon,结交朋友与劲敌,最后完成剧情任务通关,就这么简单。但是它的自由度让你可以花费大量的时间在这里面娱乐,只要你最后满足了攻略条件就可以通关,这样一款经典的冒险RPG游戏很适合作为我们的实验台。
那猴子在哪呢。
没有猴子,或者说,我们全是猴子。
口袋妖怪的第一代游戏——《口袋妖怪:红》是一代人的童年回忆,它自1996年发布之后便开始风靡全球,其后续作品至今在世界上积累了数以亿计的游戏粉丝。这位青年在直播平台上开始了重刷口袋妖怪红的直播,因为这是早年的作品,游戏的剧情设计现在看起来很简单,正常玩几个小时就可以轻松通关,但是这次不是由主播来操作角色,而是让观(hou)众(zi)们投票决定“主人公接下来该怎么做”。
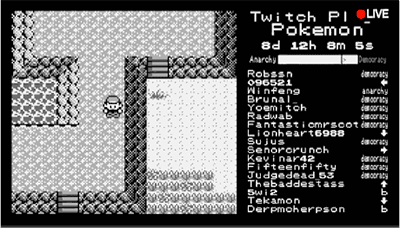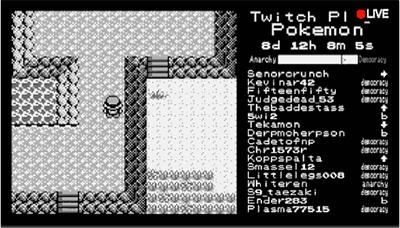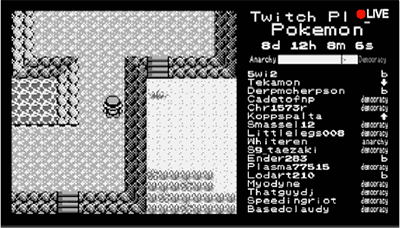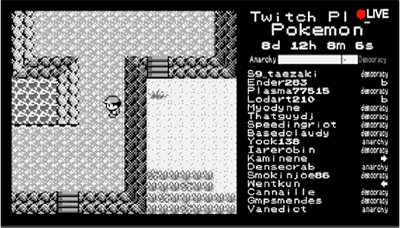
当时的口袋妖怪的操作界面很简单,只有四个上下左右的移动键用于移动和选择,以及确定键A,取消键B,举个例子,观众们投票“→”,主播就会摁下“→”键,观众们的选择也不多,主播得到的就是一串六个键位的无限重复,这个活动当时得到了两千万人的参与指令,观看直播的人数也高达十万。虽然不知道接下来会发生什么,但是大家都想去操纵主角的动作。
ABABB↑↓←A↑BA↓BB↓ABBA.......
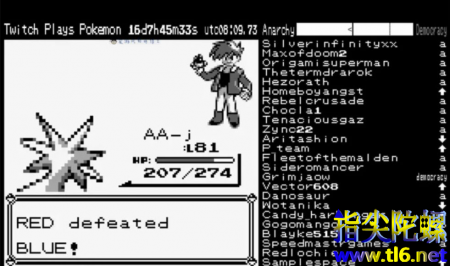
(请看最右边)
别管这是什么,按照这一串码来操作就是了。
下指令的人太多,很多相邻的指令彼此矛盾,就像是↑↓↑↓↑↓↑↓,有时候主人公想前进一步,都要花上好几分钟。我们有了足够多的输入指令,而且完全是随机分布的一串乱码,这看上去就像是一只猴子在疯狂地砸键盘,没有人能看懂它到底在写个啥。

而结果比我们想象的来得还要快,游戏开始的好几个小时后剧情终于被推进。靠着一顿乱操作,主人公居然真的通过了第一关,随后又开始第二关.....每一关用时都很长,但是可以明显看出来,千千万万个乱码最终还是将主人公引向了正确的道路。
无独有偶,前年爆火的《塞尔达》也开始了这样的实验,根据观众们提供的无数乱码,最终也让角色林克通过一阵不知名的操作(中途死亡80余次)打倒了游戏BOSS.

游戏的操作键位只有6个,而英文字母有24个,从无限的时间观念来看,猴子打出一部莎翁作品,也只是“时间问题”罢了,甚至可以说这只猴子打出的一部作品,在很久的以后,正好会是某位名家的作品也说不定(曹操:.......)
说完好玩的,就说点科学方面的。
我们通过学习概率论都知道了两件独立事的同时发生概率是二者的概率相乘,假设一个打字机有50个键,想要打出的字是“banana”。随机的打字时,打出第一个字母“b”的概率是1/50,打出第二个字母“a”的概率也是1/50,因为事件是独立的,所以一开始就打出单词“banana”的概率是:
(1/50)×(1/50)×(1/50)×(1/50)×(1/50)×(1/50)=(1/50)^6
在给定的六个字母没有打出“banana”的概率就是1-(1/50)^6。因为每一段文字都是独立的,连续n段都没有打出“banana”的概率是Xn,随着n变大,Xn在变小。当n等于100万时,Xn大约是0.9999(没有打出“banana”的概率是99.99%);但是当n等于100亿时Xn(n下标)大约是0.53(没有打出“banana”的概率是53%);当n等于1000亿时Xn(n下标)大约是0.0017(没有打出“banana”概率是0.17%);当n趋于无穷时Xn趋于零。这就是说,只要使n足够大,Xn可以变得足够小。
一只猴子太少,那就来无限只猴子!

就像一只猴子需要无限的时间打出文章,这等同于无限多的猴子中至少会有一个不负众望打出一本莎翁的书。
那么研究这些无限的定理意义何在呢?其实没有什么实用的意义,也许只是出于对无限这一宏大的概念的向往,向这种浪漫的巧合的致敬吧——宇宙如此浩大,偏偏我们都是地球上的人类,偏偏我还爱着你,这概率属实渺小,但是这就是现实,数亿年后,也许又会有一个地球,也许又会有我和你,也许我那时还爱着你。
听上去很土味是不是,实际上概率论在那些大师眼里本就不是什么高端的事情,也没有什么重大意义,对于他们自己而言,“喜欢”这一个意义就足够了。