正整数因数的个数公式
一个正整数,如果能被另一个正整数整除,就说这另一个整数是这个正整数的因数或除数。
比如,6可以被1,2,3,6都整除,所以,1,2,3,6都是6的因数或除数。
一个正整数的因数的个数是确定的,比如6的因数的个数是4;9的因数的个数是3(1,3,9)。
正整数因数的个数与这个正整数的大小没有关系,一个相对较大的正整数可能只有两个因数,比如17,而小于17的正整数12竟然有6个因数(1,2,3,4,6,12)。
一个正整数除1和它自身以外没有其他因数,就说这个数是素数。
比如,2,3,5,7,11,13就都是素数。
也就是说,一切素数都只有两个因数:1和它自身。
有的正整数有3个因数,甚至更多的因数。
那么这些数一定不是素数(是合数),反过来说也对,即有不只两个因数的正整数,一定是合数。
比如4,它是合数,有1,2,4三个因数。
再比如9,它也是合数,有1,3,9三个因数。
再比如,数16,它有1,2,4,8,16五个因数,它当然是合数。
下面我们从有确定个数的因数来反过来推导这个数是什么样的数。
先来看一看有三个因数的数是什么样子。
不难看出,有三个因数的数一定是一个素数的平方。
比如,

这个结论可以由一个数的素因数分解式及这个数的因数的个数公式得出。
我们设一个正整数n的素因数分解式为:
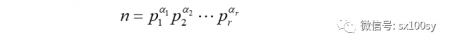
其中p1,p2,...,pr是不同的素数,α1,α2,...,αr分别是p1,p2,...,pr出现的次数,且都大于等于1。
数n的因数的个数公式为:
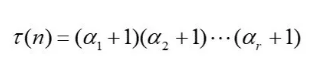
比如,
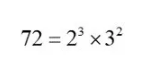
则72的因数的个数就是
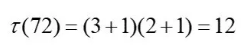
具体来说,我们可以看一看72的因数有哪些,数一数是不是12个,
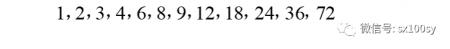
那么,刚才说有三个因数的数一定是某个素数的平方,就可以从因数个数公式推导出来。
具体来说,公式
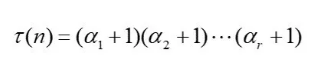
就成为
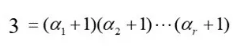
显然,上式左端为3,是一个素数,所以,右端只可能有一个因数不等于1。
也就是说上式右端只可能有一个括号。
所以,r=1,α1=2。
所以,
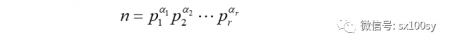
就成为
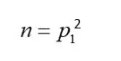
其中p1为素数。
所以997的平方994009,当然是一个很大的数,但它仍然只有三个因数:1、997和994009。
把上面因数个数为3的讨论应用于因数个数为素数,一样成立。
具体来说,因数个数公式成为:
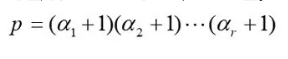
上式因为左端为素数,从而右端仍然是像p=3时那样,只有一个括号,于是同样地,r=1。
从而p=α1+1。
所以,α1=p-1。
从而因数个数为素数p的正整数就具有下面的形式:
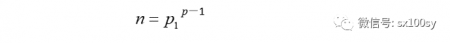
比如p=5,即n有5个因数,取p1为2(任何素数都可以),则n=2^4=16。
验证一下,16的因数有:1,2,4,8,16,确实是5个因数。
若取p1为3,则n=3^4=81。
验证一下,81的因数有:1,3,9,27,81,确实是5个因数。
下面来看一看因数个数不为素数,即为合数的情况。
比如说,有4个因数。
由
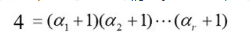
得上式右端有两个括号存在。
于是有两种情况:α1=1,α2=1;α1=3,α2=0(α1=0,α2=3的情况重复)。
于是,有4个因数的正整数的形式为:
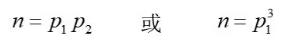
比如,

总之,根据正整数因数个数公式,可以从因数个数推知具有这么多因数的正整数是什么形式。
下面给了前一些正整数因数个数的列表:
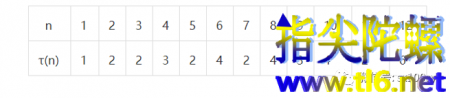
可以看出:
(1)因数个数为2的最小正整数是2,即上表中从左至右第一个出现τ(n)=2的数是2。
(2)因数个数为3的最小正整数是4,即上表中从左至右第一个出现τ(n)=3的数是4。
(3)因数个数为4的最小正整数是6,即上表中从左至右第一个出现τ(n)=4的数是6。
(4)因数个数为6的最小正整数是12,即上表中从左至右第一个出现τ(n)=6的数是12。
(5)因数个数为5的最小正整数是哪个数?个数5是素数,这个正整数应该是2^(5-1)=16。
16的因数有:1,2,4,8,16。
照此,可以得出因数个数为7的最小正数是2^(7-1)=64。
64的因数有:1,2,4,8,16,32,64。
(6)因数个数为8的最小正整数是哪个数?因数个数公式中右端应该有三个括号:8=(α1+1)(α2+1)(α3+1)。
可以是2×2×2,还可以是4×2×1和8×1×1。
从而可以对应地得出几种情况:①α1=α2=α3=1;②α1=3,α2=1,α3=0;③α1=7,α2=α3=0。
对应的正整数分别是:①2×3×5=30;②(2^3)×3=24;③2^7=128。
24是三者中最小的。
验证一下,24的因数为:1,2,3,4,6,8,12,24,共8个。
(24之前的正整数没有一个具有8个因数。
24之前的素数23,19,17,13都只有两个素数;22有1,2,11,22共4个因数;21有1,3,7,21共4个因数;20有1,2,4,5,10,20共6个因数;18有1,2,3,6,9,18共6个因数;15有1,3,5,15共4个因数;14有1,2,7,14共4个因数。)