对数平均不等式的定义与证明
关于两个正数的算术平均值和几何平均值,我们在学习均值不等式的时候就已经非常熟练了,同时我相信在讲均值不等式的时候,大家的老师一定也拓展过
与平方平均数 。同时我们也知道那么虽然我们知道了这四种不等的均值所满足的关系,但是对于我们最熟悉的几何平均值和算术平均值之间是否还有某种不等关系呢?
对数平均不等式的含义与证明
对数平均数的定义
两个正数
的对数平均数定义为 ❝这个对数平均数,正好处于几何平均数和算术平均数的中间!
❞ 那么我们应该如何证明他的确在几何和算术平均数中间呢?不等式的证明
首先当
时,结论显然成立。因此我们不妨设 ,我们先考虑(3)的右边:我们现在设
,则 ,则 ,所以函数 在区间 单调递增,故 ,从而不等式(3)右边成立。下面再证明不等式左边
由于
在设
,则 ,且等价于 .因此构造函数则
,又因为 , ,所以 在区间 单调递减,从而不等式(3)左边也成立。综上所述
恒成立。因此对数平均不等式「(A-L-G不等式)」成立。
被迫偏移的极值点
这是一个非常高大上的名称,当你说出他的时候,你会觉得自己的逼格提升了不止一个档次。

没错!他就是——「极值点偏移」
这是前几年的高考压轴题或者各个省数学竞赛预赛的常客,就因为不安分的极值点扭了扭屁股,导致无数学生为之“折腰”,但是近两年极值点偏移问题却淡出了我们的视线。为什么呢?
想一想一个可以被套路解决的问题,怎么会在此登上压轴题的殿堂呢?实际上极值点偏移问题基本上都可以通过补全法来解决,本文也就不再赘述。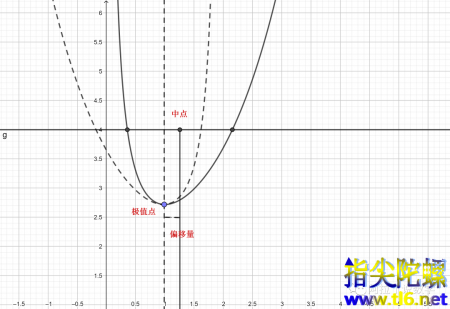
那当然是有联系的咯!废话不多说,上题!
❝已知
若 是函数 的两个零点,求证: (题源2018福建省数学联赛预赛) ❞看到这样含参数的导数压轴题,中国人的好习惯——分离变量。于是我们令
得到
做题前先画个图冷静一下
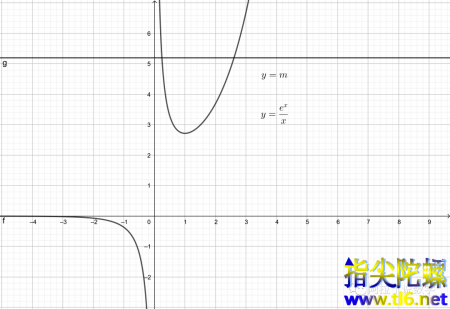
原来函数
的零点,就变成了了新函数 与 的交点,又因为题中说有两个零点,因此 与 的交点有两个(如图)。我们发现这显然是一道关于极值点偏移的问题,因为我们可爱的极值点向左稍微扭了扭屁股,我们也称之为「极值点左偏」。
现在我们来用对数平均不等式来秒杀他!
由于
为两个零点,因此有 ,而且观察图像得到只有在 的时候才会有两个交点。然后对上两式两边取对数可以得到:
因此
由对数平均不等式
因此
。证毕!虽然对数平均不等式对某些极值点偏移问题有着绝杀的效果,但是并不是所有的极值点偏移都可以通过对数平均不等式解决,而且对数平均不等式也不是为了解决极值点偏移问题产生的。
实际上在很多导数压轴题里给的条件或者要求的结果都十分奇怪,但是这种奇怪并不是不讲道理,比如学会了对数平均值不等式,你就可以造题了。比如:
❝1.求证
❞ ❝2.求证对任意的
,有 ❞学废了吗?
写在后面
很多导数题目因为对数平均不等式的存在,导致往往可以秒杀,但是在秒杀过后我更建议广大的同学们去试着分类讨论一下,因为这才是高考导数的意义所在。很多老师会在讲导数的时候讲解
展开式、 法则、甚至中值定理,但是这些工具解决高考题无异于开挂或者说高射炮打蚊子。在高中阶段我们可能更需要一种逻辑思维的训练和对未知函数分析这种能力的培养,这些超纲的办法有益于我们学习函数,但是在某种程度上却扼杀了学生探索的乐趣。总而言之,虽然处在应试教育的体系下,我们依然应该保持对数学探索,对数学的敬畏。