没有顶点,对角线怎么画?
这个题目是这样的:有一个四边形ABCD,画在一张白纸上。本来就是想简单地画出两条对角线的交点S。如下图所示。
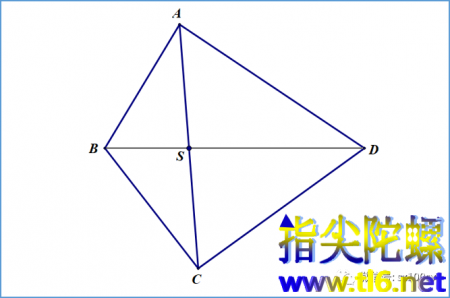
但是······不知什么原因,画有四边形ABCD的纸上,点B和点D及其外侧被撕掉了,成为下图所示的样子。
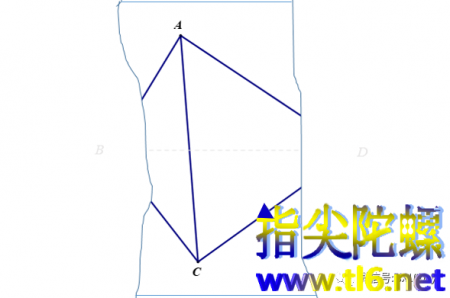
于是,虽然对角线AC仍然可以画出,但没有了点B和D,就无法画出对角线BD,从而也就无从画出对角线的交点。这可怎么办呢?小明想到了一个办法,就是把这个破损的纸片放到一张大一些的白纸上,把四边形四条边延长,从而又可以找回撕掉的点B和D的位置。这是一个好办法,也很简单。但是······,小明手头一张白纸也没有,不光白纸没有,黑纸片也没有,也没有其他可以替代之物,所以,就算有笔有尺子,也无处画线。也就是说只能利用现有的这张残破纸片。好的,情况说清楚了,也就是说,小明必须在上图所示残破纸片上画出对角线交点。
小明是个聪明的孩子,并且勤奋好学,所以他的数学水平很高。他稍微想了一想,想出了一个办法。对,利用笛沙格定理。
首先,AC是可以画出来的。在AC上任取一点P。过点P作两条直线,一条与AC左侧的两条边(或延长线)交于A'、C'。另一条与AC右侧的两条边(或延长线)交于点A"和C"。于是得到两个三角形AA'A"和CC'C"(图中阴影)。那么,这两个三角形的三组对应点A和C,A'和C',A"和C"的连线AC、A'C'、A"C"相交于一点(就是点P),所以,根据笛沙格定理,这两个三角形的三条对应边AA'和CC',A'A"和C'C",A"A和C"C的交点一定共线。这三点中,两个点就是B和D。设第三个交点为X,它是A'A"和C'C"的交点。如下图所示。这说明,点X位于点B和D的连线即对角线BD之上。并且,这个点X完全可以在残破纸片上画出。
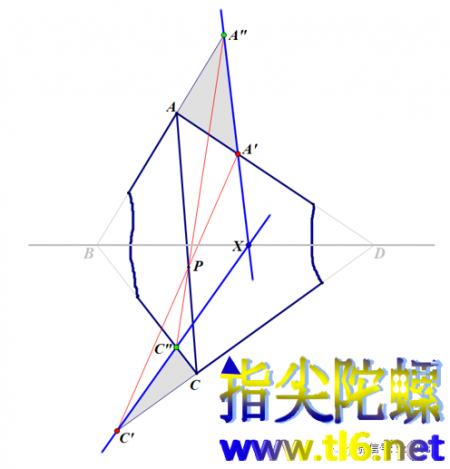
但是由于我们的纸片上已没有点B和D,而两点才能确定一条直线。所以,我们需要另外再找到一个与X类似的点。这个不难,只需在AC上另取一个与点P不同的点,按照前面的方法,就可以获得另外一个点Y。这个点Y也在BD上。所以,连接X和Y,就在残破纸片上画出了对角线BD位于残破纸片上的那部分。画出来的这部分对角线与AC的交点就是我们所求的四边形两条对角线的交点。如下图所示。
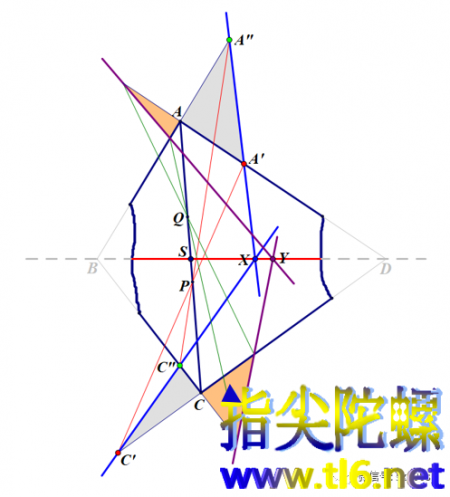
下面是动画演示。注意,这个演示的制作更加简洁,即让过点P的一条直线不动,而过点P的另一条直线绕点P转动,于是,所得到的两个三角形就在变化,从而这两个三角形的一组对应边的交点X就在变化,从而描绘出一条直线,这条直线就是过B、D的直线。
上面动画,我设置了动点的颜色动态变化,从而描绘出来的直线是一条漂亮的彩色线。
