封闭型数阵图
封闭型数阵图通常是多边形的每条边放同样多的数,使它们的和都等于一个不变的数。
1
在下图中的小圆圈中填入1~8,使得每条直线上的3个数字之和都等于14,且数字1必须在其中一个角上。
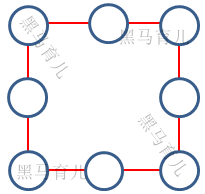
少数关键点:四个角
只有四个角上的数会被计算2次,也就是各重复1次。
解题思路:
上图中线条数是4;可用数1~8之和运用等差数列求和公式立刻知道是36;由于四个角上有一个是1,假设其他三个角的数字之和是s,那么有:
14×4=36+(1+s)
s=19
2~8里选择3个数,使之和为19,则由加减奇偶性可知,必然是3个奇数,或者是1奇2偶。如果是3个奇数,2~8里只能是3、5、7,但它们之和不为19,所以我们只能看看1奇2偶了。
考虑到之和是19,也只能存在2个可能:5、6、8或者是4、7、8
①如果四个角分别是1、5、6、8
1、5必须是对角,否则它们之间的数字只能是8,冲突了;
1、8必须是对角,否则它们之间的数字只能是5,冲突了。
上述两个条件相互冲突,所以这个不成立。
②如果四个角分别是1、4、7、8
1、4必须是对角,否则他们之间数字是9,超出范围。既然如此,后续填写就非常容易了:
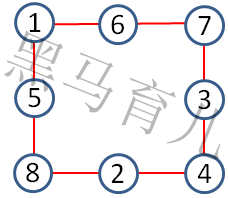
2
下图中的小圆圈中的每个字母分别代表1~8这8个数字,且每条直线上的3个数字之和都相等,那么d、e两个数字之差是多少?
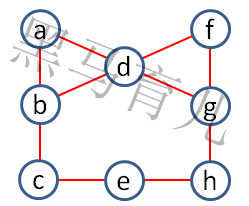
少数关键点:e
因为其他任何一个小圆圈都处于2条直线上,也就是会被计算2次,只有e只会被计算1次。
解题思路:
与之前学的大多数情况不一样,这次的少数关键点是没有被重复计算的,而其他数字都被计算了2次。
上图中线条数是5,除e以外其他数字都算了2次;可用数1~8之和运用等差数列求和公式立刻知道是36;假设每条直线上的3个数字之和是s,那么有:
5s=2×36-e
5s=72-e
由于5的倍数只能是5、0结尾,所以e只能是2或者7,那么d是多少呢?已知e了,也就知道c和h之和了,再来观察一组式子:
(a+b+c)+(f+g+h)=2s
(a+b+f+g)+(c+h)=2s
又因为:
(a+d+g)+(b+d+f)=2s
(a+b+f+g)+2g=2s
所以我们可以很清楚的看到:
2g=c+h
当e是2的时候,s是14,也就是c+h=12,g=6;
当e是7的时候,s是13,也就是c+h=6,g=3;
两种情况下,d、e之差都是4