四面体的质心在哪儿?
今天讲一个简单的知识,那就是四面体的质心(也叫做重心或中心)。我们要证明一个四面体每个顶点到对面中心连线(叫做四面体的中线)相交于一点,且这点到顶点距离与到对面中心距离之比为3:1。
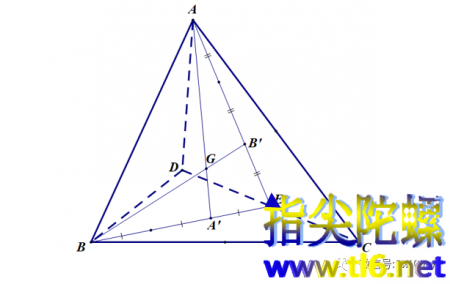
我们知识,在平面时,三角形三条中线相交于一点,这点叫做质心(或重心、中心),质心把中线分成2:1两部分(到顶点为2,到对边中点为1)。那么为什么在空间时,质点分中线却是3:1呢?怎么证明?
如上图所示,BE是三角形BCD中从点B发出到达边CD中点的中线,AE是三角形ACD中从点A发出到达边CD中点的中线。点A'是三角形BCD的质心,点B'是三角形ACD的质心。所以,BA':A'E=2:1,AB':B'E=2:1。连接AA'和BB',则AA'和BB'分别是四面体之三角形BCD和ACD上的中线。AA'和BB'的交点设为G。为了研究问题方便,我们观察三角形ABE,如下图中的阴影。并连接A'B'。
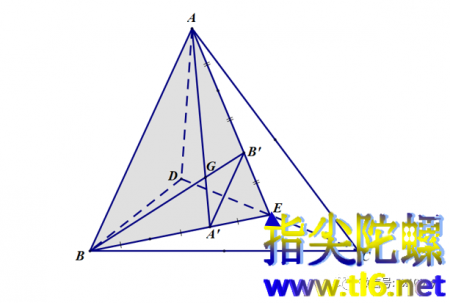
如上图所示,显然三角形ABE与三角形A'B'E相似,相似比为3:1。又三角形ABG与三角形A'B'E相似,所以AG:GA'=BG:GB'=AB:A'B'=3:1。即点G同是中线AA'和BB'的四等分点。同理可以证明四面体其他两条中线都经过点G。并且点G把四条中线都分成3:1两部分(到顶点为3)。所以最终我们就证明了四面体四条中线交于一点,且这点把四条中线每条都分成3:1的两段(到顶点为3)。证毕。
下面给出另一种证法,它非常简洁。如下图所示。
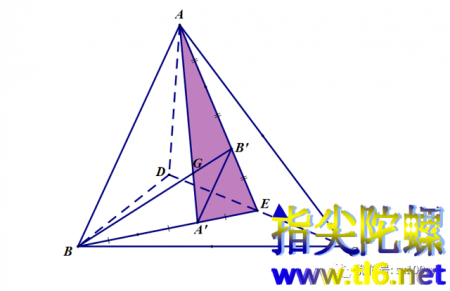
我们观察上图中的阴影三角形AA'E。它的三条边(或延长线)AA'、A'E、EA上分别有三个点G、B、B',且这三点共线。根据梅涅劳斯定理,有
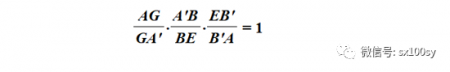
即
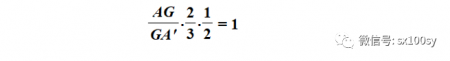
所以
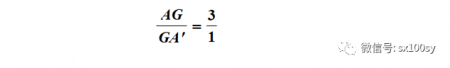
证毕。
四面体的质心还有另一种方法得到:四面体有四条棱,两两相对成异面直线,构成三对对棱。可以证明四面体三对对棱中点连线相交于一点,且这点是三条连线的中点。可以进一步证明这个点就是四面体的质心。
(1)首先证明四面体三对对棱中心连线交于一点且这点平分每条连线。如下图所示,PP'、QQ'、RR'为三条对棱中点连线。很容易证明红线所示为平行四边形。所以,它的对角线相交且互相平分,设交点为G',那么PG'=G'P',QG'=G'Q'。同理点G'也是RR'的中点。
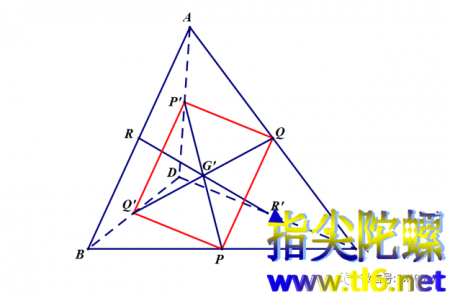
(2)下面我们假设已经按照前面的方法得到了四面体的质心G。然后我们来证明点G就是对棱中点连线的中点G'。如下图所示,在上上张图的基础上,连接EG,并延长,与AB交于点S。设EG与A'B'的交点为T。如下图所示。我们分两步走,第一步是证明G为SE的中点,第二步证明点S就是AB中点。
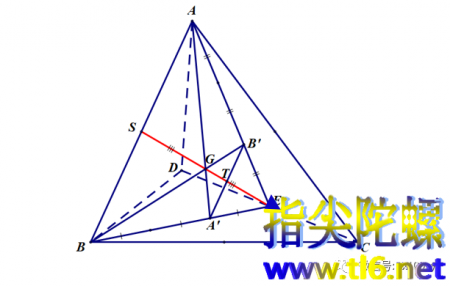
(3)由三角形EA'B'与三角形EAB的相似比为1:3,知ET:ES=1:3。所以,若设ET为2份,那么ST就是4份。再由三角形GA'B'与三角形GAB的相似比为1:3,得GT:GS=1:3。那么,ST这4份中,GT占1份,SG占3份。于是,GT+TE就占3份。所以,SG=GE。即G为SE的中点。

(4)再来证明点S为AB中点。证明过程中反复应用“三角形面积等于底乘高除以2”及“高相等时,底的比值就是面积的比值”。这里,因为EB':B'A=1:2,所以,若假设三角形EB'G的面积为1份,则三角形AB'G的面积就是2份。从而三角形EGA的面积就是3份。再由SG=GE,得三角形SGA的面积也是3份。再由三角形EA'G的面积与三角形BA'G的面积之比为1:2,及三角形EA'A的面积与三角形BA'A的面积之比为1:2,可以得出面积差也是这个比例,即三角形EGA的面积与三角形BGA的面积之比也为1:2。所以,三角形BGA的面积就是6份。所以,三角形BGS的面积也是3份。从而三角形BGS与AGS的面积相等,所以BS=SA。即点S为AB的中点。

最终,我们便证明了四面体质心G也是对棱中心连线的中点G'。所以,三对对棱中点连线相交点G'就是质心G。
(5)其实,从力学的角度看问题,假设在四面体的顶点处各放置一个质量都为1个单位的质点,那么质点A和B的质心就位于AB的中点S处,质量为2个单位。同样地,质点C和D就相当于在CD中点E处放置一个质量为2的质点。那么,“两点棒AB”与“两点棒CD”的平衡点即质心就是AB中点与CD中点连线的中点。从另一方面考虑,三个等质量质点的质心在以三个质点为顶点构成的三角形的质心处,质量为3。四面体三个顶点的质心与第四个顶点(也放置一个同质量质点)的平衡点自然就位于三角形质心与第四个顶点连线的四等分点处,离三角形质心与离第四顶点的距离之比为1:3(反比),而这个点正是四面体四条中线的交点即质心G。