倍立方体的制作
今天讲一个很有趣也很实际的问题,您若有兴趣也有条件,可以用木块或其他材料自己动手制作。
有两个棱长为1分米(10厘米)的正方体木块,并且我们还有一根木杖,它的长度是
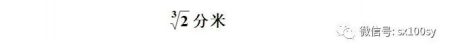
请您用这两个棱长为1分米的木块为材料,对它们进行切割再拼接,而成为一个正方体。要求切下来的块再拼接时块与块之间不能有空隙,并且没有材料的浪费(锯木块产生的木屑忽略不计)。
这个问题看上去不就是倍立方问题么!但数学上的倍立方问题是研究是否可以用尺规作图作出倍立方体的棱长(已证明这个问题是尺规作图不能问题,其他两个也是尺规作图不能的问题是:三等分角问题和化圆为方问题)。而我们这里假设倍立方体的棱长已经知道。所以,本问题其实已不是倍立方问题了。所以从数学上来说已没有太大困难了。只不过这里是处理立体图形,做法上有些费事,但确实很有趣,并且实践感很强。而最后一共切割了多少块的问题,还是很具有挑战的。
好的,我今天在这里讲解这个过程。如下图所示,有一个任意的平行四边形ABCD和一条长度为(2的开3次方)分米的线段EF。
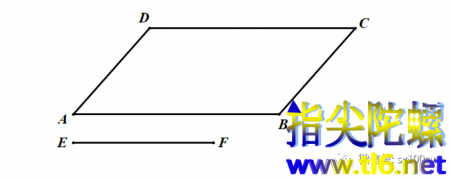
(1)如何在面积不变的基础上,调整一个平行四边形(矩形属于平行四边形,我们后面对其操作的正是矩形)不同方向两边的长度(不改变方向)使其有一边长度等于已知长度?比如,在上面这个平行四边形ABCD中(不妨假设AB>CD),就需要调整AB边长度使其减小到与EF(不妨假设大于平行四边形长边的二分之一)同长度。我们真正要做的是把原平行四边形进行切割,然后把切割出来的几块再拼接成一个两条不同边夹角不变但一边长度为EF的另一个平行四边形。(拼接问题当然都是假设拼接前后的图形的面积不变。)
步骤:在AB上截取AG=EF。在CD上截取HC=EF。连接BH并延长,与AD的延长线交于点J。过点J作AB的平行线,与过点G所作与AD平行的直线交于点K。设GK与BH的交点为L。如下图所示。
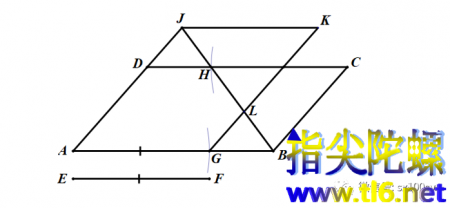
显然,GB=DH,所以三角形GBL与三角形DHJ全等。而三角形BCH与三角形LKJ也全等。所以,可以把平行四边形ABCD沿BH剪开,再沿GL剪开。把三角形GBL平移到三角形DHJ处,再把三角形BCH平移到三角形LKJ处。从而原平行四边形就剪拼成平行四边形AGKJ。如下图所示。
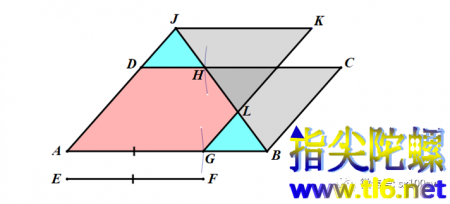
(2)下面开始把两个棱长为1分米的正方体切割和拼接成一个棱长为(2的开3次方)分米的大正方体。我们将两次应用上面这个切割拼补方法。
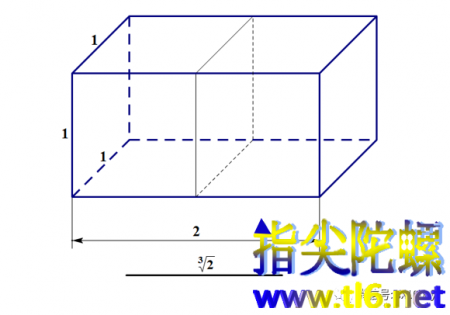
对面向我们的这个长方形面ABCD实施第(1)条中的切分(划线):先取点G使AG等于定长(2的开3次方)分米,再取点H使HC等于同一定长。连接BH。过点G作AB的垂线,与BH交于点L。于是,BH和GL把矩形ABCD分成三块:五边形AGLHD,三角形GBL和三角形BCH。
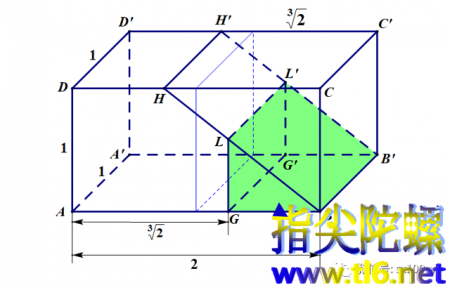
分别过点H、L和G作BB'的平行线段HH'、LL'和GG',其中H'、L'和G'都位于背面A'B'C'D'上。连接H'L'、L'B'和G'L'。于是,我们便得到三个直棱柱:五棱柱AGLHD-A'G'L'H'D',三棱柱GBL-G'B'L'和三棱柱BCH-B'C'H'。上图中我们给三棱柱GBL-G'B'L'标以颜色,然后其他两块也就容易看得出来了。下一步我们把这三个直棱柱切割开来。然后,把三棱柱GBL-G'B'L'平移使GBB'G'与DHH'D'重合;再把三棱柱BCH-B'C'H'沿着BH方向平移,使BB'与LL'重合。于是我们就得到一个新的长方体。如下图中AGG'A'-JKK'J'所示。
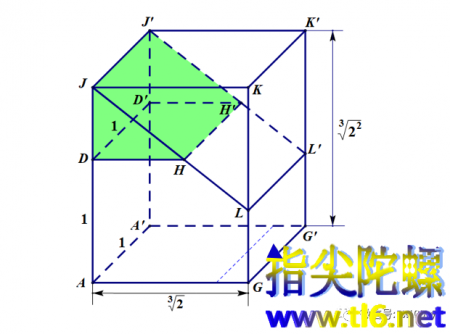
原来两个边长为1分米的正方体的总体积是2立方分米,我们上面对它们所作的切割和拼接,几个小块之间没有任何空隙,也没有任何浪费,拼成另一个长方体。这个长方体的AA'方向的棱长度仍为1分米,AG方向的棱长度为(2的开3次方)分米,所以,GK方向的棱长度一定是(2的平方再开3次方)分米,因为
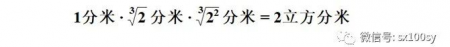
(3)下面我们先把上图中的切割线隐去(颜色很浅,且为细线)。然后对这个长方体再进行切割与拼接,便可以得到一个边长为已知长度的正方体即倍立方体。我们从下图出发。
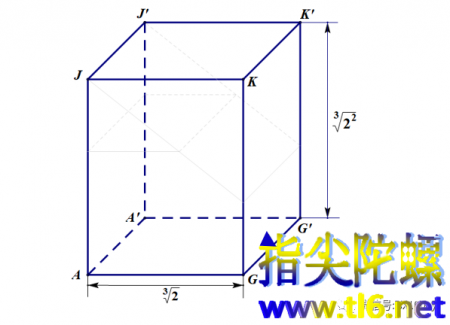
AG长度已正确。所以,需对GG'和G'K'进行调整。GG'和G'K'位于长方形GG'K'K上面,所以,我们对这个长方形进行类似前面的处理。在GK上截取GM=AG,在G'K'上截取K'N=AG。连接KN。过点M作KK'的平行线,与KN交于点P。于是,我们把长方形GG'K'K分成三块:五边形GG'NPM,三角形MPK(图中内涂蓝色)和三角形NKK'(图中内涂红色)。如下图所示。
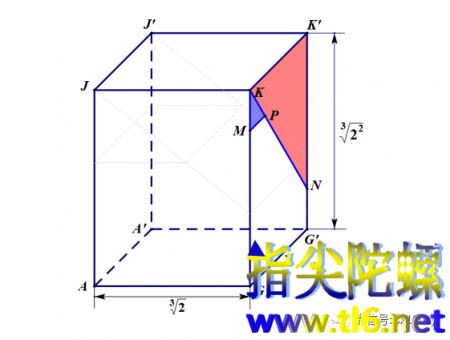
延长KN,与GG'的延长线交于点Q。分别过点M、P、N、Q作AG的平行线,分别与对面即AA'J'J所在平面交于点M'、P'、N'、Q'。连接JP',P'N',N'Q',M'P',A'Q'。于是,我们便得到三个直棱柱:五棱柱GG'NPM-AA'N'P'M',三棱柱MPK-M'P'J(蓝色),三棱柱NKK'-N'JJ'(红色)。
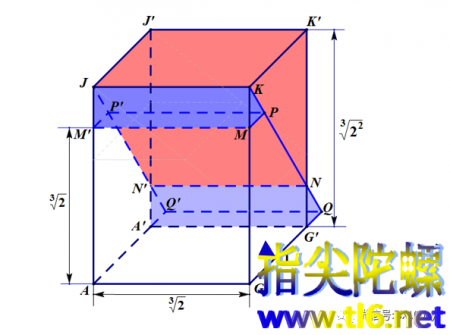
把三棱柱MPK-M'P'J(蓝色)沿KN平移KN长度至图中浅蓝色三棱柱的地方,再把三棱柱NKK'-N'JJ'(红色)沿KP平移KP长度。最终得到的结果便是倍立方体AGGA'-M'MRR'。
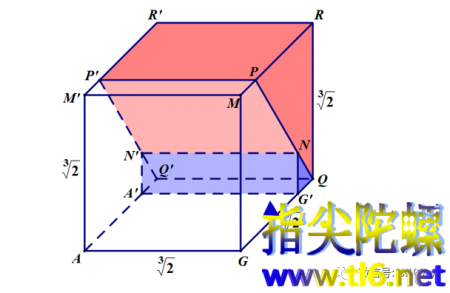
(4)最后一问:这个倍立方体是由多少块拼接成的?也就是问,把原来两个棱长为1分米且粘在一起的两个正方体(算作一个1×1×2长方体),按上述两次切割步骤共切出了多少块?
按照我上面的做法,答案是8块。请您参考下图,我把这8块一一给您列出。下图中的长方体AGG'A'-JKK'J'是第一次切割并拼接后所得,它由三块构成:五棱柱AGLHD-A'G'L'H'D',小三棱柱DHJ-D'H'J',大三棱柱LKJ-L'K'J'。注意,两次切割操作每一次都是“两刀”,下面所说都是指第二次切割操作中的“两刀”,其中一次是沿着N'NKJ这个面(图中的红色平行四边形,实际上是矩形),第二次是沿着M'MPP'这个面(图中粉色平行四边形,实际上也是矩形)。因为第一刀切掉大三棱柱NKK'-N'JJ',所以第二刀再切掉小三棱柱MPK-M'P'J时不会切到大三棱柱NKK'-N'JJ'。
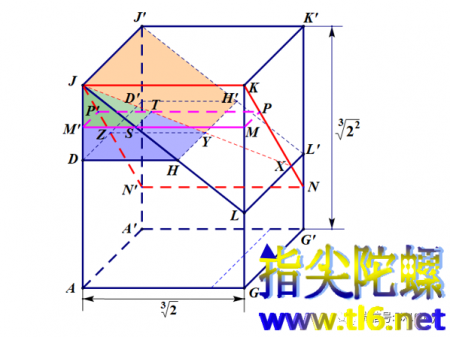
我们先来看红色切割面这一刀,它与原来的大三棱柱LKJ-L'K'J'的交线是JX(因为红色切割面上的线段KN与三棱柱LKJ-L'K'J'上的斜面LL'J'J上的线段LL'有交点X,点J也是两个面的交点之一,所以,根据两个平面交于两点,则它们必定交于过这两点的直线这一性质,这条直线的一部分JX就是两个面的交线)。那么,我们就很容易看出大三棱柱LKJ-L'K'J'被切割成了两部分:五面体XKJ-L'K'J'和四面体XKJ-L(请您在上图中找一找)。对五面体XKJ-L'K'J'来说,粉色四边形切割面不会切割到它,所以,这一块就已经是8块之一了)。我们记它为:第①块:五面体XKJ-L'K'J'。对四面体XKJ-L来说,它与粉色切割面相交,所以,这个四面体必定被切割成两块,并且这两块就是最终的,成为8块中的两块。观看下图,这两块是:第②块:五面体MPK-STJ。第③块:五面体LMS-XPT。

以上对大三棱柱LKJ-L'K'J'的切割的分析就完成了。下面研究小三棱柱DHJ-D'H'J'被切割的情况。看一看红色切割面把小三棱柱DHJ-D'H'J'切割成哪些块。点Y在红色切割面上,点Y也在小三棱柱DHJ-D'H'J'的DHH'D'面上;另一方面,点Z既在红色切割面上,又在小三棱柱DHJ-D'H'J'的DHH'D'面上。所以,线段ZY就是红色切割面与小三棱柱DHJ-D'H'J'的DHH'D'面的交线。而JY是红色切割面与小三棱柱DHJ-D'H'J'的JHH'J'面的交线,所以,三角形ZYJ就是红色切割面切割小三棱柱DHJ-D'H'J'产生的切割面。这就是说,红色切割面把小三棱柱DHJ-D'H'J'切割成了两块:一块是五面体ZYJ-D'H'J'。它以后不会再被切到了,所以,它将成为8块中的一块,我们叫它为第④块:五面体ZYJ-D'H'J'。另一块就是四棱锥J-DHYZ。而这一块不是最终块,它还将被粉色切割面横切一刀,得到两块。这两块就是:第⑤块:小四棱锥J-M'STP'和第⑥块:四棱台DHYZ-M'STP'。

最后的第⑦块和第⑧块来自五棱柱AGLHD-A'G'L'H'D'。但从上图不太容易看出来,我把上图改造一下,如下图所示。从图中您去发现一个七面体。这个七面体的四个面(左右侧面和上方的两个面)被涂色了,而正对着我们的面我没有涂色,空着。于是可以看到里面,看到垂直的背面A'G'NN',看到被红色切割面切出的五边形面N'NXYZ,看到底面AGG'A'。所以一共是七个面。但确实不太好用项点字母表示,因为用字母表示感觉不出是几面体。最后一块是一个六面体,我就不特别画它了,它在七面体的后面,字母表示为:N'NXYZ-L'H'D'(像是一个以N'N为交线的二面角)。
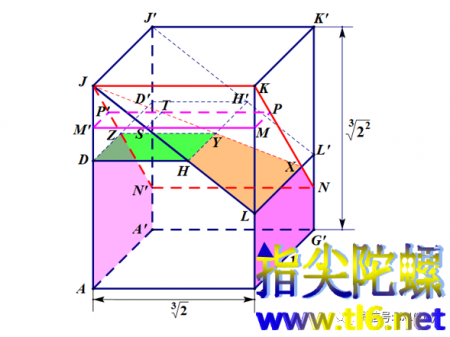
以上我讲解了“8块”的情况。通过以上讲解,我们可以对空间面与面的交线怎么找怎么画有一些认识。
但若先把第一次切割后的长方体上下颠倒过来再进行第二次切割,则答案是7块。就我所知,7块可能是目前最少块数。有对此问题研究更加深入的朋友,可以留言交流。谢谢!
若把“8块”或“7块”打散,再拼出正方体,感觉还不一定很容易。所以,可以做成玩具。