因式分解在找规律中的应用
发布时间: 浏览: 次 作者:www.tl6.net
上次介绍过桥上搭桥,每座桥上的规则完全不一样,另外还有一种,是将数字因式分解后,每个因子各自有各自的规律。
第一题: 1、4、9、20、40、78、()
还是老办法,在直接观察看不出数字之间规律,也不存在跟平方、立方相关的时候,我们还是在每两个数字之间“搭一座桥”,并在桥上标记这2个数字之间的关系,如下图所示:
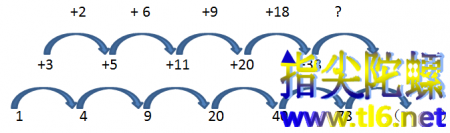
很显然,看不出任何规律,即便第三层,还是看不出规律,所以我们尝试对数字进行因式分解看看。
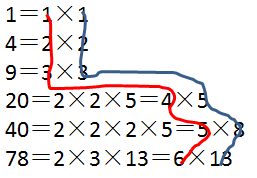
从因式分解结果看,我们找出其中一组1、2、3、4、5、6,剩余另外一部分因子能组成另外一个数列:1、2、3、5、8、13。

在《找规律·找数字规律(二):搭桥法介绍》中,我们介绍过这个数列,用搭桥法,能看出来桥上的数字跟桥下正好错位,向右错了一位。实际上这个数字就是斐波那契数列(就是从第三个数字开始,后面一个数是前面2个数字之和)。
回到原来的题目,78=6×13,所以后面一个数字就应该是7×21=147