布里安香定理 | Gergonne点 | 塞瓦定理
(1)先给出后面要用到的塞瓦定理。
塞瓦定理:三角形ABC中,点D、E、F分别位于边BC、CA、AB上。那么,三条塞瓦线AD、BE、CF共点的充要条件是:
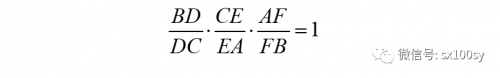
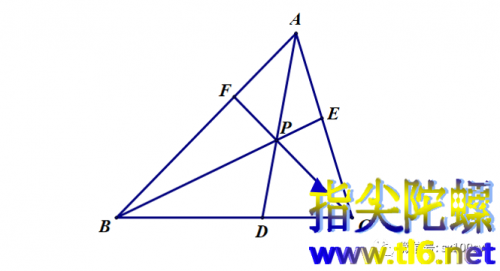
(2)本期介绍Gergonne点。设三角形的内切圆与三条边相切之点分别为D、E、F(注意,这里的D、E、F三个点不一定是角平分线与对边的交点)。下面简单证明三条塞瓦线AD、BE、CF共点,这个点叫做Gergonne点(下图中点G)。(注意,点G与内心I是不同的,虽然有可能挨得很近。)
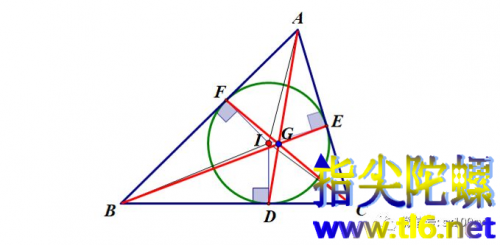
因为D,E,F三点都为切点,所以有
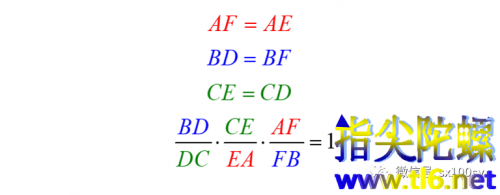
根据塞瓦定理充分性,这样的三条塞瓦线是共点的。这个点就是所谓的Gergonne点。
(3)用布里安香定理证明上述三线交于一点,则是显然的。用到的是布里安香定理中外切六边形每相邻的两条边成为一条边时,这时的六边形变为三角形,原相邻两条边的交点及这两边与圆锥曲线的相切点,三点合一,成为合并之边与圆锥曲线的切点。这时的布里安香定理成为:三组顶点与对边上的切点的连线共点。下图中,AD、BE、CF交于点S。那么在圆锥曲线为圆时,三条线的交点就是上一条所说的Gergonne点。
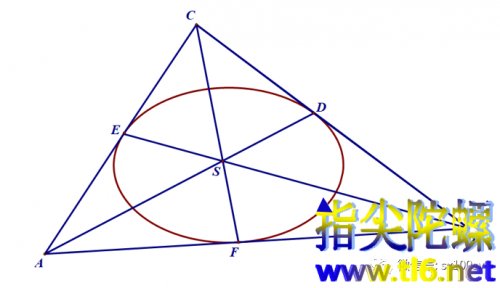
布里安香定理对椭圆等全部圆锥曲线都是成立的,而Gergonne点第一个证明中用到的“圆外一点到圆的切线相等”就太过特殊了。但是,说特殊也并不很特殊,因为椭圆可以当成的圆的仿射变换,所以,对圆正确的结论,只要不涉及长度、角度等具体度量值,对仿射变换成的像,布里安香定理这个射影几何学的定理,也是成立的。具体来说,在原像中,圆与三边的切点分别把三边分为成比例的两段,然后,经过仿射变换,圆与外切三角形都变形了,变为了椭圆及它的外切三角形,但三边中的切点仍然分这边为相同比例的两段,所以,三个比例相乘后仍然等于1,所以塞瓦定理依然成立。如下图所示。注意下图中三个比例的乘积等于1。
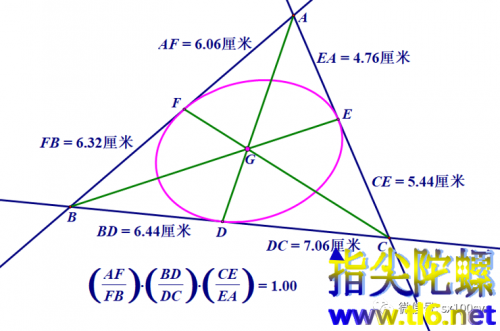
所以,我们可以称上图中点G也为Gergonne点,那么你说这个三线共点是巧合吗?一点也不巧合,对圆锥曲线都成立,是世界中存在的客观规律。