帕斯卡原理定律及其各种变化情况
今天讲对偶的帕斯卡定理,读懂每一幅图。
一、椭圆情况
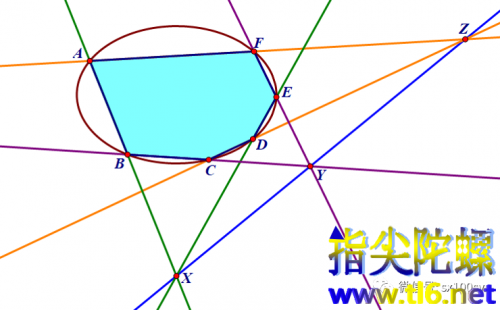
1-1 ABCDEF为椭圆内接六边形。
相对之边AB与DE(无C和F)相交于点X,BC与EF(无D和A)相交于点Y,CD与FA(无E和B)相交于点Z。
那么X、Y、Z三点共线。
如下图所示。
(图中六边形看上去其点A远离其他五个点,不够任意,这是为了使X、Y、Z能够全部显示在图中。
若是任意,就有可能X、Y或Z跑得很远,不利于图示。
)
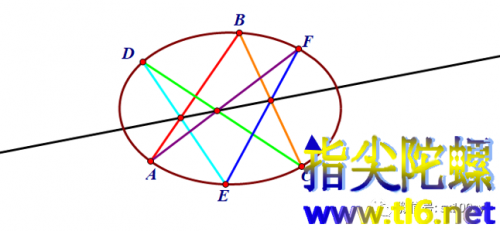
1-2 ABCDEF不一定是上图那种我们常认为的凸六边形。
下图的ABCDEF也是六边形。
注意字母的顺序(我还用无黄色(黄色太浅)的七色给出点的走向),那么AB的对边仍然是DE,BC的对边仍然是EF,CD的对边仍然是FA。
但这并不影响帕斯卡定理的正确性。
如下图所示。
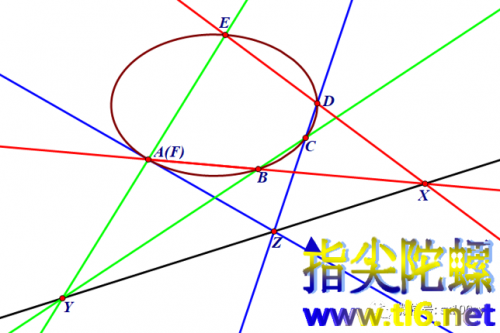
1-3 ABCDE为椭圆内接五边形。
五条边中任意选定两组对边,其中一组对边AB与DE(红色)交于点X,另一组对边BC与EA(绿色)交于点Y,那么第五条边CD(蓝色)与和它正对顶点处切线(蓝色)的交点Z一定位于X与Y确定的直线(黑色)上。
如下图所示。
其实这就是六边形情况下让点A与F重合。
(本题可以用来找椭圆上一点处的切线,这里是点A处的切线。
具体方法是:除点A外,再在椭圆上找四个点B、C、D、E,按下图中的方式确定点X和Y;然后作过CD的直线,它与直线XY交于点Z;最后连接AZ,则AZ就是点A处椭圆的切线。
)
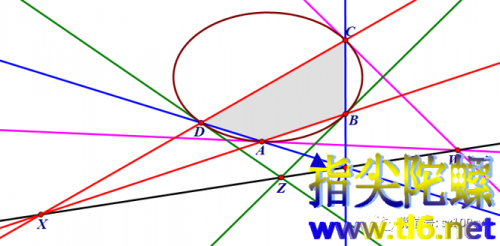
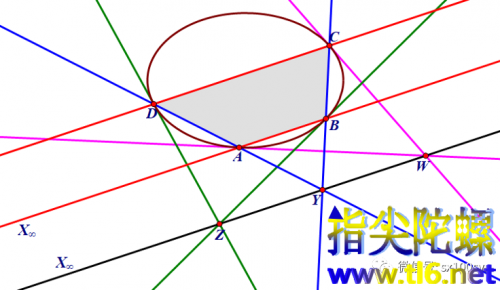
1-4 ABCD为椭圆内接四边形,对边AB与CD交于点X,对边BC与DA交于点Y,对顶点B与D处的两条切线(可以看作六边形的两条对边都退化成点)相交于点Z,对顶点A与C处的两条切线相交于点W,那么X、Y、Z、W四点共线。
如下图所示。
(其实是根据帕斯卡定理,X、Y、Z三点共线,而同理X、Y、W三点也共线,所以才有四点共线。
)
1-5 若椭圆内接四边形ABCD中有一组对边平行,比如AB∥CD(这时可认为交点为无穷远点X∞,那么上面1-4的帕斯卡定理依然成立,只不过X∞、Y、Z、W四点共线具体表现为另外三个交点Y、Z、W共线,且这条所共之线与AB(及CD)平行。
如下图所示。
(注意,X、Y、Z、W中任何一点都可成为无穷远点。
这里不再一一列举。
)
1-6 ABC为椭圆内接三角形。
这时可以也把这个三角形看作是六边形的特殊情况:六边形三条相间的边仍在,而另三条相间的边都缩为点。
那么这时原六边形的每一组对边就成为现三角形的一边与它的对顶点处的切线。
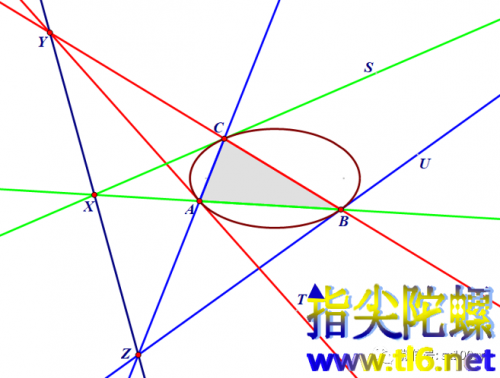
于是,针对椭圆内接三角形的帕斯卡定理就成为:椭圆内接三角形三边分别与对顶点处切线相交出三个点,那么这三点共线。
具体来说,如下图所示,边AB与切线CS的交点X,边BC与切线AT的交点Y,边CA与切线BU的交点Z,则X、Y、Z三点共线。
1-7 对椭圆内接三角形也有平行及无穷远点的情况。
若AB与CS平行(可认为交点在无穷远点X∞),而BC与AT的交点仍为Y,CA与BU的交点仍为Z,那么AB平行于XY。
图略。
二、双曲线情况
2-1 内接六边形6个顶点取在双曲线的同一支上,帕斯卡定理肯定正确。
如下图所示。
2-2 上面2-1的极限情况——双曲线变成它的渐近线,那么便有了帕普斯定理。
如下图所示。
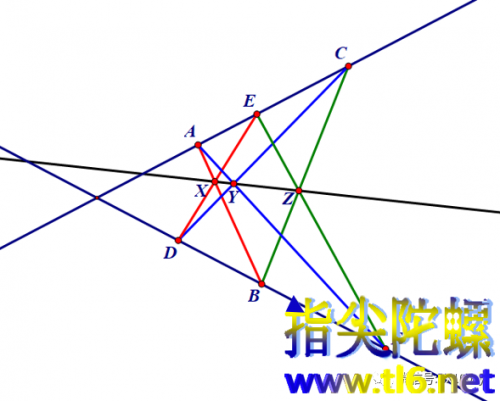
2-3 6个顶点中三个取在左支上,3个取在右支上,同样正确。
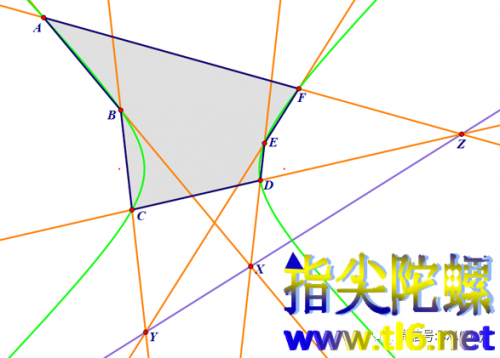
如下图所示,AB与DE的交点X,BC与EF的交点Y,CD与FA的交点Z,则X、Y、Z三点共线。
其实,6个顶点的顺序是任意的,只要任意三个点不在一条直线上即可。
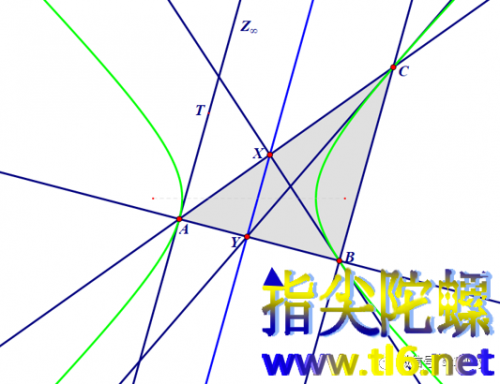
2-4 A、B、C为双曲线上三点,不妨设A位于左支,B和C位于右支。
则三角形ABC为双曲线的内接三角形。
连线BC,再作点A处的切线AT。
设点B处切线与对边AC相交于点X,点C处切线与对边AB相交于点Y,点A处的切线与对边BC交于点X,那么,三点X、Y、Z共线(图略)。
这里给出一种特殊情况,即如果点A处的切线AT与BC平行,那么XY也与AT及BC平行。
当然,我们同样可以说X、Y、Z位于同一直线上,只是这里的点Z跑到了无穷远处成为Z∞。
2-5 双曲线内接四边形ABCD的变化情况比较多。
我们举个例子,这例子以前是就着椭圆讲的,这里我就着双曲线来讲,并且只用到帕斯卡定理,全可以解释得通,很好理解。
神奇得很!如下图所示。
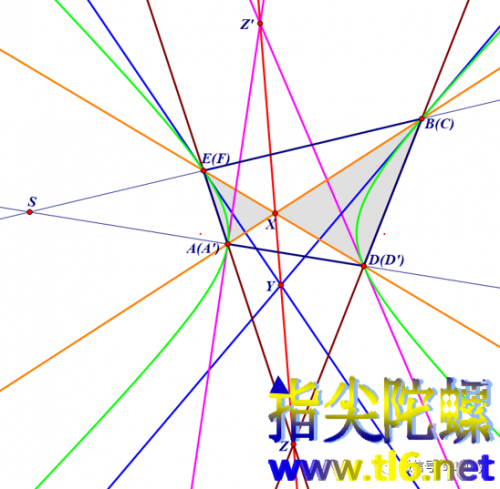
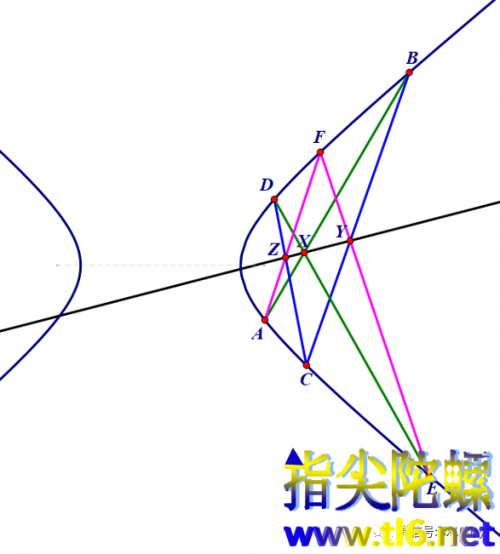
从一点S引双曲线的两条割线,分别与双曲线交于A、D和E、B。
我们按ABDEA的顺序构造一个内接四边形(注意,是图中阴影的边界)。
若把B点当成B、C两点的重合点,把E点视为E、F两点的重合点,那么内接四边形ABDE就是内接六边形ABCDEF的退化形式。
于是三组对边交点共线。

我们来分析是哪三组对边。
第一组是AB与DE(橙色)(C空过去,F也空过去),相交于点X;第二组是BC与EF(D空过去,A空过去),两者都已退化为切线(蓝色线),它们相交于点Y;第三组为CD和FA(褐色)(缺E和B),它们相交于点Z。
X、Y、Z共线(红线)。
另外,由点S所引任意一条割线将与双曲线交于两点,那么,这两点处的切线的交点的轨迹就是这条所共之线XY。
点S与直线XY之间是极点与极线的关系。