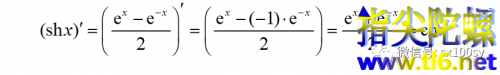悬链线方程的推导过程、求解及应用
今天讲一讲悬链线。把一根质量分布均匀的链子或软绳的两端系在等高的两个点上(其实不等高也不影响),则链子或软绳自然弯曲而成的曲线就是悬链线。很早以前人们认为悬链线是抛物线,因为看上去确实很像。但后来物理学家和数学家都证明了它不是抛物线。根据力学原理分析悬链或软绳的受力,可以得出悬链线的方程是:
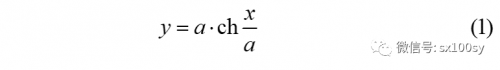
其中涉及双曲余弦:
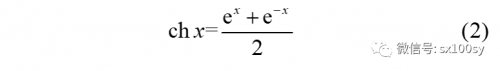
类似地,还有双曲正弦、双曲正切:
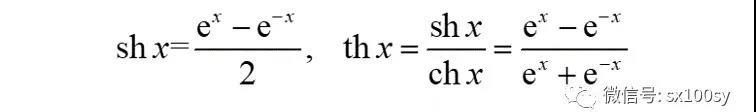
双曲正弦、双曲余弦、双曲正切及双曲余切(cthx=1/thx)统称为双曲函数(或双曲线函数)。双曲函数有一些性质后面会用到:
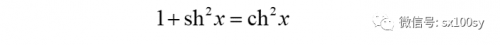
|
证明如下:
|
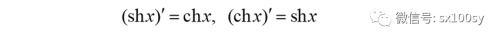
|
证明过程如下:
|
悬链线的图像关于y轴对称,顶点坐标为(0,a),是悬链线的最低点:
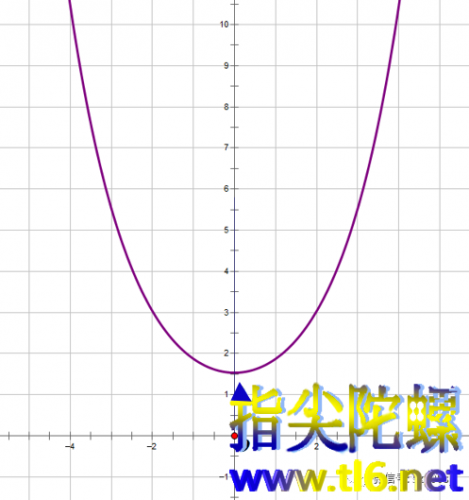
下面我们看如何作悬链线上任意一点处的切线。求导数,得:

我们假设切线已经作出,那么,过点P向x轴引垂线,设垂足为B。过点B向切线作垂线,垂足为C。则有
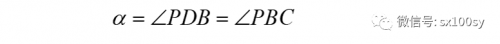
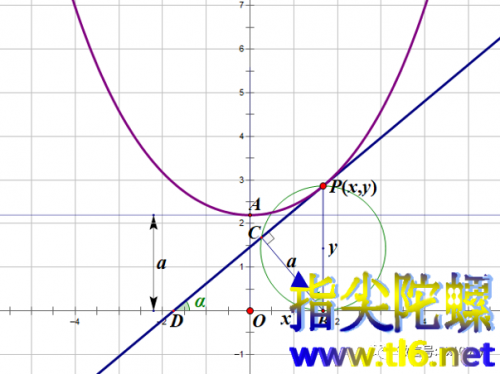
所以,
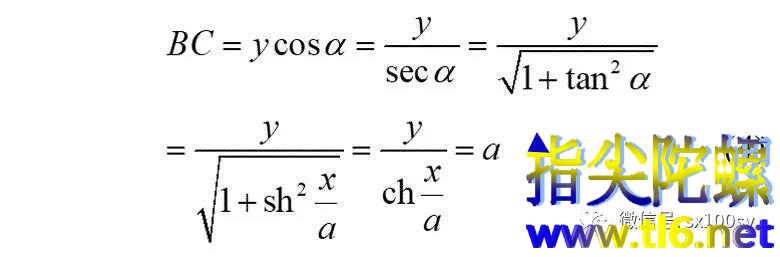
上式的推导用到了已得结果(3)及双曲函数shx与chx之间的平方关系(前面有推导)。BC正好等于a,这提示我们,可以这样作悬链线上一点P处的切线:过点P向x轴作垂线,垂足为点B。以PB为直径作圆O。以点B为圆心,以a为半径作圆O',与圆O交于点C。则过P和C的直线就是悬链线过点P的切线。
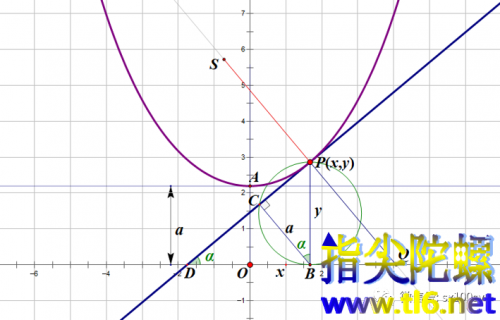
观察上图,容易得出法线长度为:
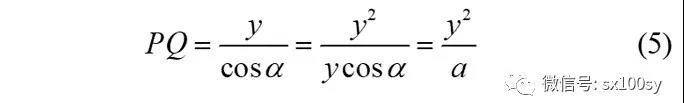
再根据曲率半径公式:
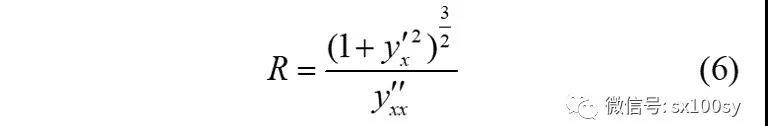
可以得到点P处的曲率半径为:
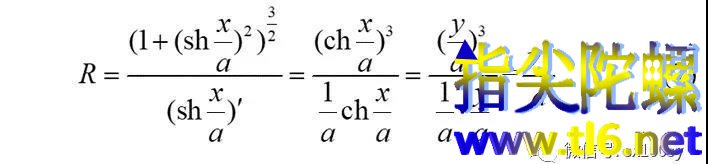
即曲率半径等于这点处法线长度。所以,我们可以容易地从法线找出曲率中心S(上图中红点)。那么,也就可以画出曲率中心的轨迹即悬链线的渐屈线(下图中红色曲线)。注意,渐屈线永远与法线相切,或者说,渐屈线是法线的包络。切点S就是曲率中心。这个渐屈线像不像飞向我们的海燕!
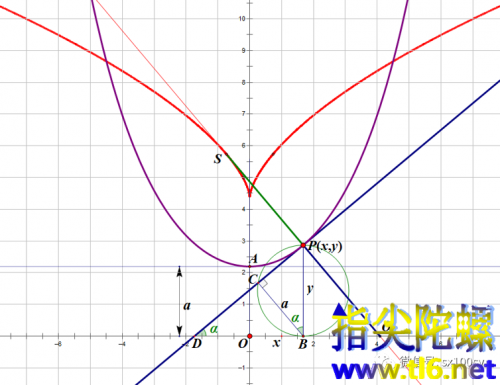
下面我们再来计算从顶点A到任意一点P的曲线长度。

再由(3)式,即
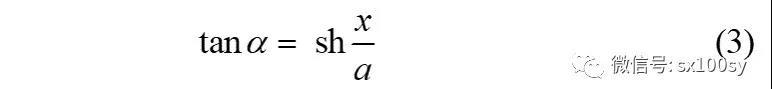
得到
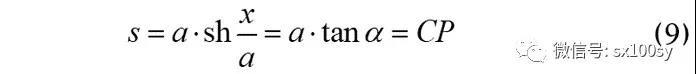
于是,由于曲线弧长AP的长度不好测量,我们就可以转换成测量直线段CP的长度。我们还是像前面那样,先做出点P在x轴上的投影点B,以PB为直径作圆O,以点B为圆心以a为半径作圆O',与圆O交于点C。连接CP。则CP的长度就等于弧AP的长度。我们只需测量线段CP的长度即可。或者这样做也行:如下图所示,以顶点A为圆心,以点P的纵坐标y为半径作圆O",与x轴交于点E(本是有两个交点,我们取与P在y轴同一侧的交点)。则得到直角三角形AOE。那么,OE的长度就是弧AP的长度。
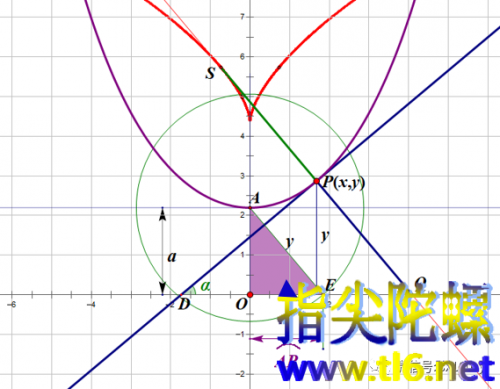
本期内容,既有高等数学的微积分,又有初等数学的几何作图。很难得!