伯努利双纽线
(1)起源。我们熟悉的椭圆是这样定义的:到两个定点的距离之和等于定长的点的轨迹。这里定长2a必须大于两定点间距离2c。雅各·伯努利仿照椭圆的定义,稍做改动,发现了双纽线。他是这样定义双纽线的:设两定点F、F′之间距离为2a,则到两定点距离之积为定值a²的点的轨迹就叫做双纽线。双纽线的图形如下图所示,它的形状像个横着的“8”,也像是无穷符号“∞”。
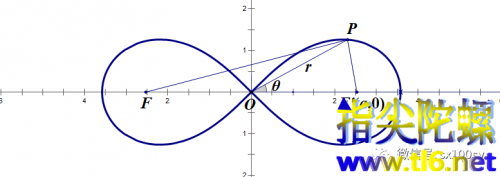
(2)方程的推导。双纽线的极坐标方程不难得到:

(3)性质。显然,极点到两定点的距离的乘积=a²,满足定义。所以双纽线过极点。再由方程看出必须cos2θ≥0。所以
0≤2θ≤π/2
3π/2≤2θ≤5π/2
7π/2≤2θ≤4π
推出:
0≤θ≤π/4
3π/4≤θ≤5π/4
7π/4≤θ≤2π
所以双纽线位于x轴上下但夹在与x轴正向成±45°角的两条直线之间。如下图所示。
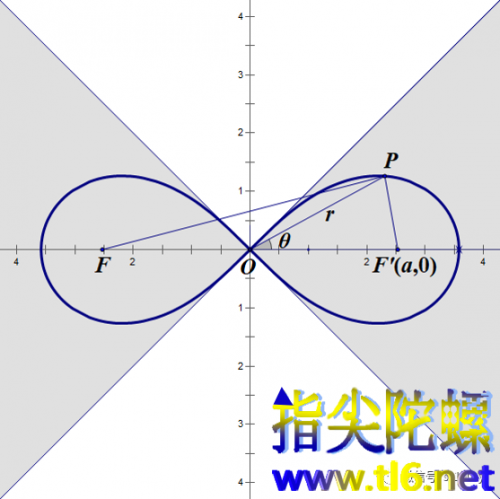
(4)所有双纽线都是相似的。把方程作一个变形,得到:

此式说明,a放大或缩小,r也等比例放大或缩小。这就是相似的定义。
(5)画双纽线的切线和法线。设μ为双纽线上某点处切线方向与这点处的向径的夹角。于是
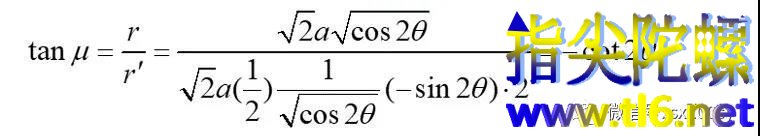
得到
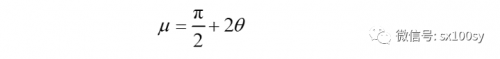
而又有
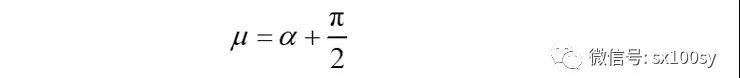
所以

所以


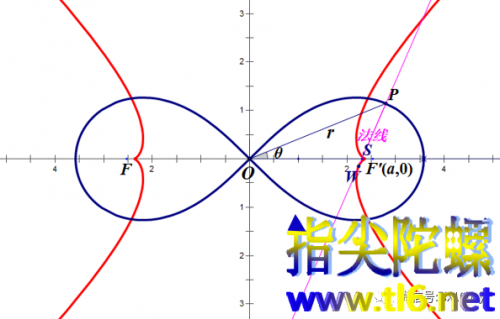
这个结果使得我们能够作出双纽线的法线。作法:在向径一侧作出两个θ角,得射线OQ。再过点P作OQ的平行线,与x轴交于点S,则PS即为法线。法线的倾角就3θ。
我们知道曲线上一点处的曲率就是这点处密切圆的曲率(曲率半径的倒数)。根据公式可求出曲率中心(如下图中的点W)。从而我们可以得到双纽线的渐屈线(曲率中心的轨迹),见下图中的红线。双纽线的渐屈线没有什么特色,一般书上都不讲。它的样子与双曲线有些接近,但在x轴上出现了尖点。尖点与两定点很接近,但稍微靠近内侧。
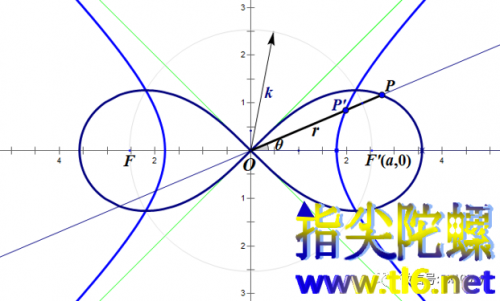
(6)双纽线的反演是双曲线。说到双曲线,我们下面就来讲一讲双纽线的反演图形。通过用k²/r代替r(其中k²为反演幂),可推导出反演图形的方程:

这正是双曲线,且是特殊的等轴双曲线,如下图蓝线所示。等轴双曲线以直线y=x和y=-x为渐近线,如下图中的绿线。从上面方程可以看出,不管反演幂k²是多少,反演图形都是等轴双曲线。
(7)若双纽线定义中定值a²改为b²(b不一定等于a),那么动点的轨迹就是所谓的卡西尼卵形线。b>a时为一个大“卵″形,b<a时为两个对称的小“卵”形。b=a时就是双纽线了。见下面的动画。
(6)图形面积。提供三种计算双纽线所围区域面积的方法。先说前两种,后一种放到文章最后。第一种是极坐标下的一元定积分(曲边三角形面积之和的极限)方法;第二种是二重积分(可以用二重积分求一个区域的质量,当区域质量均匀且单位面积的质量为1时,二重积分就是面积)。我们只给出公式推导结果。
①极坐标下定积分求面积。由公式
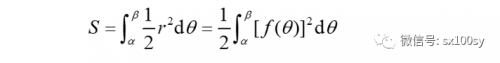
得
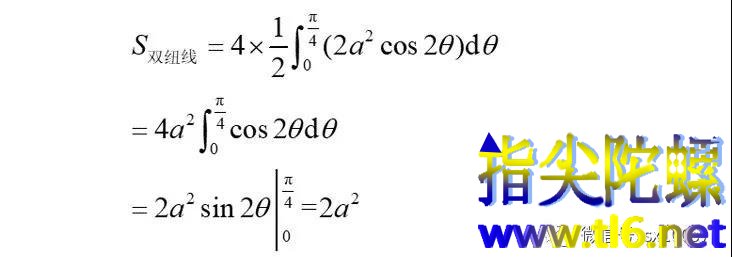
②二重积分求面积。由公式
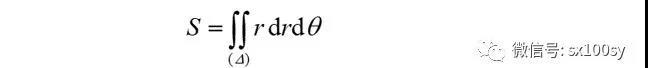
及双纽线极坐标方程(θ从0到π/4):
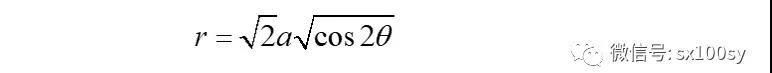
得
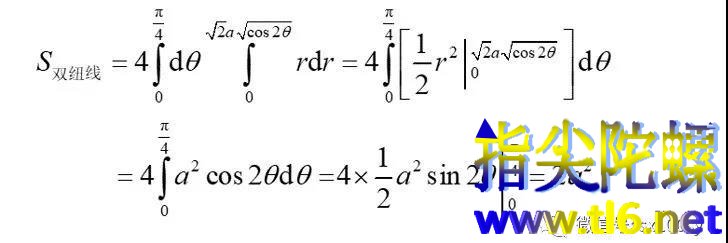
把②中二重积分的面积单元拉长为扇形单元,就变成了第①种方法。都是相通的!
(7)双纽线的直角坐标方程不难推导:
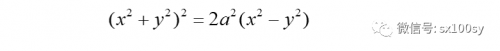
双纽线的极坐标方程为:
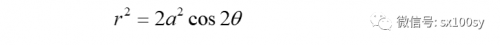
上网搜“双纽线的极坐标方程",有时式中少了系数“2”,这是因为对a的定义不同,如下图所示:
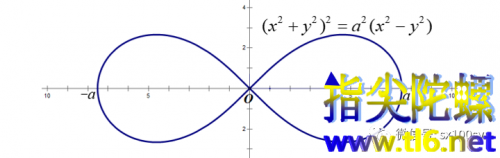
原因是无“2”的方程中a是双纽线与x轴交点的横坐标绝对值,是两定点之间距离一半的根号2倍。这样设a可能是与椭圆的情况类似。这也有道理,因为椭圆标准方程中也是出现了a和b,而没有出现焦距的一半c。
(8)第三种求双纽线面积的方法:利用双纽线的参数方程及曲线积分。不妨就把极角θ当成参数,根据x=rcosθ和y=rsinθ,得
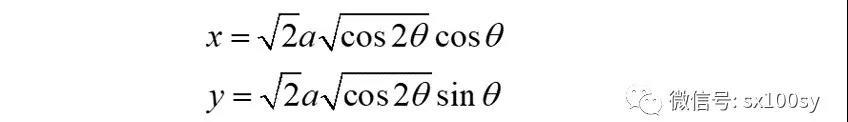
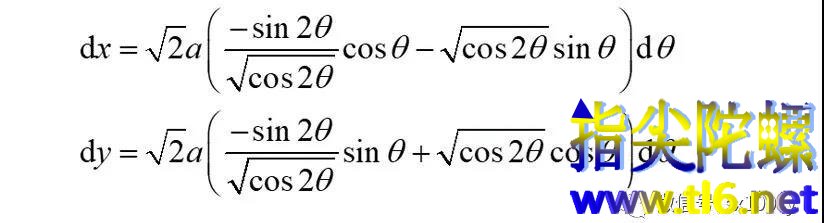
所以,
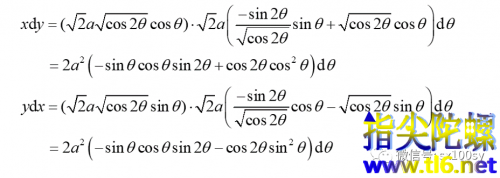
于是,我们就用曲线积分先求出一个纽的面积,再乘以2,就得“双纽”的面积。

可以发现,不管是哪种积分求面积,在用牛顿-莱布尼茨公式计算前,被积函数的样子关键部分是一样的(cos2θ)。最终都归为普通的一元定积分。