麦克劳林三等分角曲线
今天简单讲一下麦克劳林三等分角曲线,及它是如何做到三等分一个角的。
(1)作抛物线:
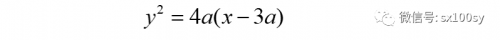
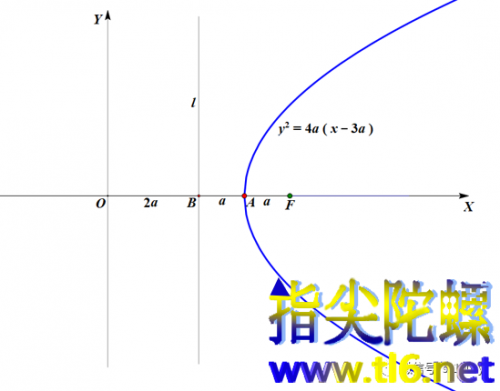
(2)在抛物线上任取一点P。作点P处抛物线的切线m。从点O作切线m的垂线,垂足为M。
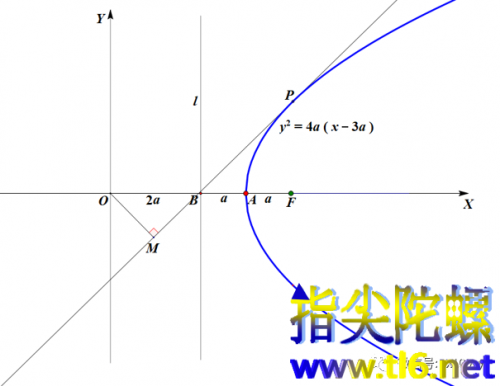
(3)让点P在抛物线上运动,那么,垂足M的运动轨迹就是所谓的麦克劳林三等分角曲线。(有关垂足曲线的知识,在前两三期的内容中有过介绍。)麦克劳林三等分角曲线见下图中的红色曲线。(注意,这条曲线是无限的,这里是因为作图原因没有画全。)
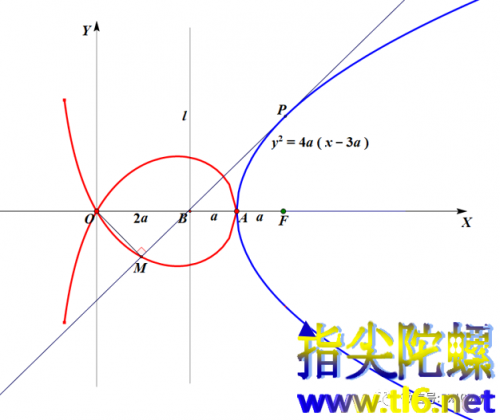
(4)这个麦克劳林三等分角曲线这么叫,说明它主要是用来解决三等分角这个三大尺规作图不能问题之一的。那么当然,我们就要讲清楚这条曲线是怎么解决一个角的三等分问题的。
(5)必须要讲麦克劳林三等分角曲线的方程。第一步是写出过点P(x,y)的抛物线切线方程。第二步,写出垂线方程。第三步,求出切线与垂线的交点M的坐标,从而求出点M的运动轨迹的方程。下面就是简单的过程。
把抛物线方程两边对x求导,得:
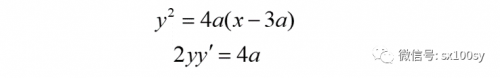
从而得出过点P的切线m的斜率:
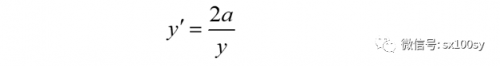
于是,由点斜式方程,求出切线的方程为:
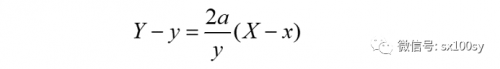
那么,过点O且与切线垂直的直线即垂线n的方程可以求出(其斜率为切线斜率的负倒数):
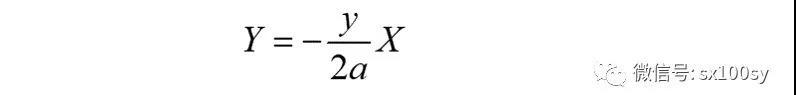
注意,大写的X和Y是切线和垂线的自变量。
到此时,我们求出了抛物线上某一点P(x,y)处的切线方程,也求出了过一定点且与切线垂直的直线方程,那么,两条直线的交点即垂足也就可以求出。垂足的坐标一定是用切点的坐标x和y来表示的。但切点在抛物线,即x与y是相互制约的,这种制约就体现在抛物线方程。从而,垂足的坐标实际上都是受切点的一个坐标(x或y)的影响。于是,垂足坐标X和Y都是用参数x(或y)表示的,即参数方程。那么消去参数,就将得到垂足的直角坐标方程。所以,最终,我们只需从抛物线方程及上面求得的切线方程、垂线方程这三个方程
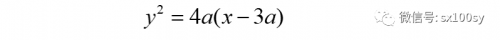
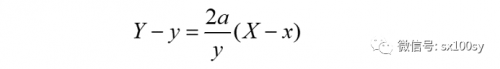

消去参数x和y,就可以求出点M的运动轨迹的直角坐标方程(具体过程省略):

(6)若以麦克劳林三等分角曲线内部的点B(准线与x轴的交点)为极点,BX为极轴,那么,我们来推导麦克劳林三等分角曲线的极坐标方程。在曲线上取一点Q(X,Y),如下图所示。则有
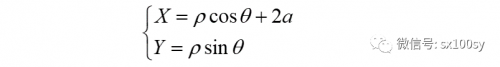

把上式代入曲线的直角坐标方程中,得

(上式中运用的三倍角公式,可根据两角和的余弦公式推得)从上面最后一式中,第一个因式即中括号中的式子一般不等于0,只有当ρ=a时,才等于0。而在ρ=a时,θ=0。这种情况包含在了上式第二个因式中。所以,我们就推导出了麦克劳林三等分角曲线的极坐标方程为第二个因式等于0,即:

即

(7)这个方程是麦克劳林三等分角曲线可以解决三等分角问题的关键。怎么解释呢?我们把要被三等分的角置于极坐标系中,让角的顶点与极点B重合,让角的一边BA与极轴重合。那么,角的另一边就与麦克劳林三等分角曲线交于一点Q。这点的极坐标就是Q(ρ,θ)。我们要对其进行三等分的角就是∠ABQ。注意,下图中角θ的标注是指∠ABQ。
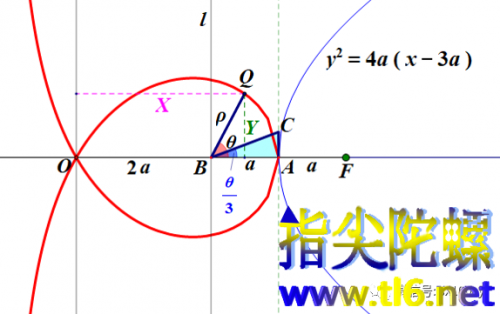
如上图所示,作一个以BA边为一直角边,以A为直角顶点,斜边长度为ρ的直角三角形ABC。由方程

立即看出,∠ABC=θ/3。所以,线段BC就是∠ABQ的三等分线之一。就这么简单!
本篇内容公式推导很多,这种数学运算能力需要具备。