超静定与瞬变体系有没有关系?
一、力学模型的视角
超静定这个词汇在理论力学和材料力学中提的多,而瞬变体系则在结构力学中谈的比较多,那么这二者有没有联系呢?
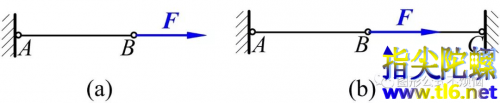
图1
看图1(a)中AB(本文所讨论的杆件均为不计重量的轻杆)。按认知习惯,对这种问题,只讨论沿杆方向的外加载荷(图中F),而不讨论垂直于杆的载荷。此时AB的内力是确定的。
图1(b)在图1(a)的基础上添加了一根水平杆BC【为了简洁(但不失概念准确性),取AB=BC】。按从图1(a)到图1(b)的认知定势,F仍然是沿水平方向。
图1(a)的力系沿一条直线(为了方便阐明概念,KFC使用了最简单模型),所以只有一个独立方程。利用这一独立方程,可定出了AB的受力--这是静定问题。
图1(b)是从图1(a)的拓展而来的,认知习惯会沿袭图1(a)而认为它是直线力系。但是,它的一个方程就无法求出AB和BC两根杆的内力,所以这就是静不定问题。
在图2(a)中,一出手就是两根杆。此时结点B受到平面汇交力系而平衡,可以写出两个独立方程,从而可求出AB和BC两根杆的受力。
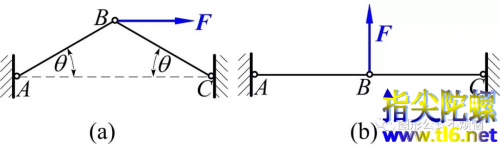
图2
如果把图2(a)的θ设为0,就变成图1(b)。如果沿这条线走下来,那么图1(b)则为瞬变体系。在考虑了杆的变形后,图1(b)两杆内力可确定,而且为有限值。
然而,如果从图2(a)的结构出发,按习惯载荷就不能只限为水平,竖直也会有分量。为了简单起见,图2(b)中只作用力有竖直方向的F。这就是典型的瞬变体系。两杆内力会变成无穷大。在考虑了材料变形后(考虑变形后ABC便不在一条直线上),AB和AC的内力可以定出,但也会相当大——所以瞬变体系在结构上很危险。
二、线性代数的视角
下面通过线性方程组解的类型,来体会超静定和瞬变体系的区别和联系。
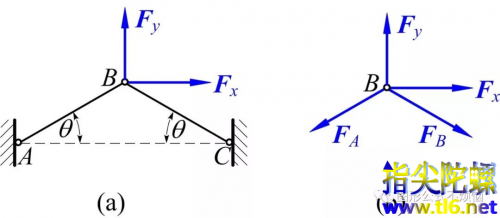
图3
图3(a)的B点受力既有水平分量,也有垂直分量。取结点B做受力分析,如图3(b)所示。列平衡方程

当|M|≠0时方程组(2)有唯一解,这对应静定情形。该情形的sin2θ≠0°。
当|M|=0时,有θ=0°(另一解θ=90°要求AB和BC为无限长,不用讨论),此情形下方程(2)变成
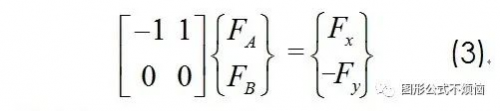
如果Fy≠0,则方程(3)无解,这相当于图2(b)的情形。此时肯定为瞬变体系。
如果Fy=0,则方程(3)有无穷多解,这相当于图1(b)的情形。这就有两个视角。如果从图1(a)出发,此种情形可称为超静定,相应地在我们思维定势中竖直方向的力和位置变化都不用考虑。
另一个视角是图2(a)退化为图1(b),那么在这个视角下,图1(b)就是瞬变体系。
对Fy≠0,方程(3)无解。在数学上,也可以想象成解是趋近于无穷大的极限。在工程上,由于材料的变形和装配误差,θ接近于0但不精确等于零,这造成的后果就是FA和FB会很大。
总结如下:线性方程组有唯一解对应静定问题;没有解对应瞬变体系;有无穷解则有两个视角,静不定和瞬变体系都可。
根据以上分析图4右边为瞬变体系。如果右边的2P换成也改成P,也可说成是超静定(思维定势是内部A'B'C'一开始就假定它没有旋转的自由度和相应外载荷)。
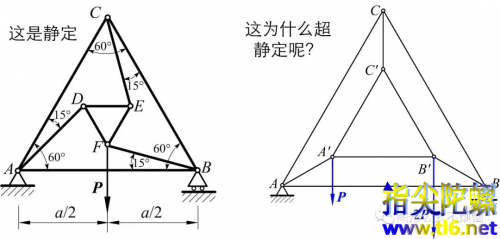
图4