什么是反函数?反函数的定义,反函数怎么求导?
高中阶段在研究函数的过程中总是会碰到十分复杂的内联嵌套问题,比如
.这类函数有抽象函数也有具体函数,在分析其零点问题的时候,很多同学会相当的头疼,既不能画图,也不能写出相应的解析式那可怎么判断呀?
其实这类很复杂的函数有一个很专一的考点——函数零点,正所谓独特之处必成考点,联系之处必有解法。函数的零点其实也就是方程的根,亦或是两个函数的交点,从这个角度出发,我们就可以绘制出复杂函数零点分布的简单草图。
什么是反函数?
在进入主题之前,我们要再次回顾高中阶段一个很边缘化的知识点——反函数。
❝设
为数集,
为双射,则对每个
都有唯一确定的
满足
。按照映射的定义,这也就定义了一个新的映射
,称之为
的反函数,其表达式为
.
❞
而且值得注意的是
是
上的恒等变换,因此
也是
的反函数,故
但是函数或者映射是允许“多对一”但不允许“一对多”,因此任何一条竖直直线与函数曲线至多一个交点,因此我们可以得到一个重要的结论:
❝严格单调的满射,必有反函数,且
严格增时,
也严格增。严格减时亦然。
❞
简单来说就是将函数的定义域与值域发生互换,但是必须遵循映射的一般原则,这在几何图形上反应在原函数图像与反函数图像关于
对称。
高中阶段最著名的互为反函数的一对函数就是对数函数和指数函数,可是细心的同学会很快发现,反函数的适用面非常小,只有严格单调的函数才可能有反函数,那么在处理具体情况中非常复杂的嵌套函数怎么能利用到反函数的图像呢?
一切函数都是分段函数,一切函数都是单调函数
高中阶段我们主要研究的函数相对来说比较简单,这也就是我们学习导数的目的更注重判断函数的单调性,那么在各个不同的单调区间上,每一个函数都是单调的。这正是将函数分割,整体化局部的思想。
正所谓一切函数都是分段函数,一切函数都是单调函数。如果有这样的分割思想,那么在相应的单调区间画出反函数图像不就很轻松了吗?但是还是要说明一下,这样画出的对称反函数图像已经不是一个函数了,显然它存在了“一对多”,但是交点和单调区间依然保持,因此这样的草图对判断零点问题非常有帮助。
例题分析
例1.
已知函数
则关于
的方程
可能会有多少个实根?
拿到这样一道题相信大多数同学是发懵的,有少数同学会发现这个分段函数的解析式并不难,我们可以试着复合一下,也就是计算麻烦一点。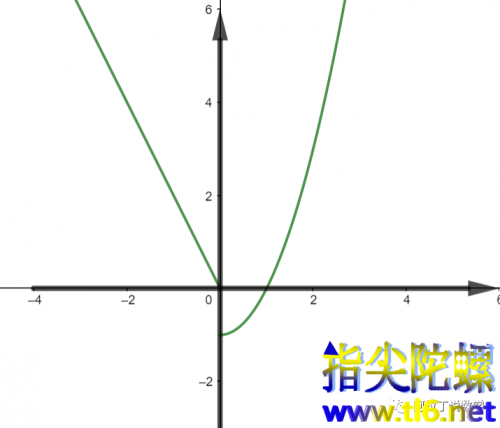
那么我们把原方程变一下:
,我们只需要求
的表达式即可。
首先就是分段,在
时
;在
时,
因此不难算出
绘制图像可得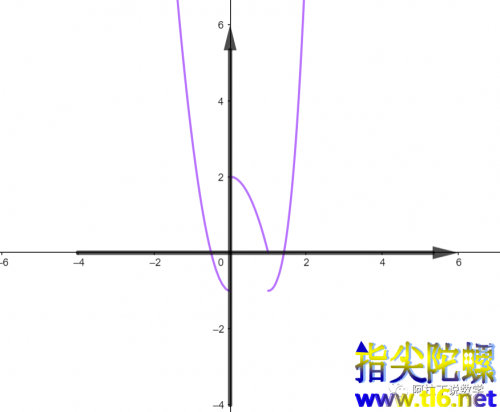
时,方程有一个实根;当
或
时,方程有两个不等的实根;当
时,方程有三个不等的实根。
这种做法无可厚非,但是前提是这种程度的复合是可以接受的,计算量不算太大,而且都是多项式函数。但是如果出现了更加复杂的函数形式,这种做法可能就捉襟见肘了。
所以观察到方程
形式非常好,我们把它变换一下
,这就转化成了求
的反函数在
处的函数值,进而观察
的图像,这个函数值和原函数的交点个数就是原方程的零点个数。
我们将
分段,保证每一段都是单调函数,保证了每一段都有对应的反函数,将所有反函数结合,得到了一个曲线(这里不能叫函数),但是为了表述方便我们依然称其为
的图像,入图所示
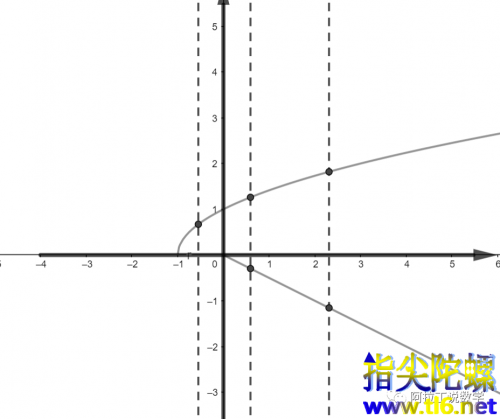
当
时,如图所示
与
的图像的交点
;当
时,如图所示
与
的图像的交点$0<y_0<1$;<section=""></y_0<1$;<>当
时,如图所示
与
的图像的交点
或
当
时,如图所示
与
的图像的交点
或
注意这里由于反函数与原函数的定义域与值域发生了变化,所以反函数的
就变成了原函数的
.因此这时的交点
,也即将其带入到
的图像中去寻找交点,如图所示
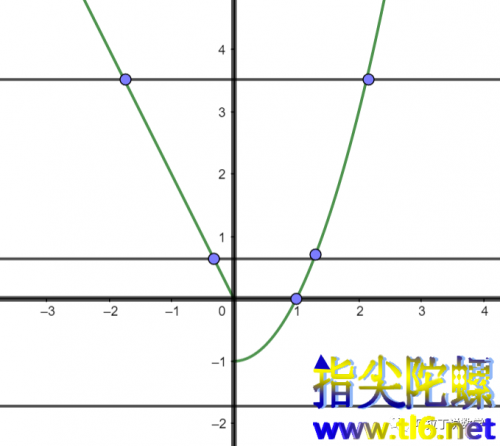 当
当
时,
仅有一个交点;当
时,
有两个交点;当
时,
有两个交点,当
时,有一个交点,因此总共三个交点;当
时,同上,但是
时,无交点,因此总共只有两个交点。
综上所述,方程
可能会有1个、2个或者3个根。
相信大家看到这里会提出不少疑问,这个例子其实算是很简单的,因为
的分段都是单调函数,在求交点的过程中会轻松不少,那么我们就来看一个稍微复杂一点的。
例2
已知函数
则函数
的零点个数为多少?
这道题就比刚才复杂的多,在分析根的成因的时候也相对不容易。那么还是以我们刚才说的函数的零点就是两个函数的交点就是方程的根这个思想来分析。
的零点个数就等价于
的根的个数。
我们可以这个嵌套的函数一层层剥离来看,不妨设内层函数
,则
,做出
的大致图像,如图所示
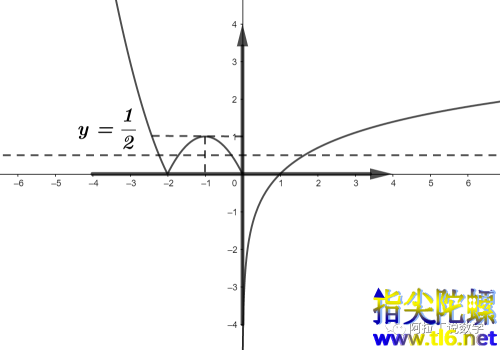
则
有4个实数根
,其中
;
;
;
接着来看外层函数,若
,则
有1个实数根;若
,则
有1个实数根;若
,则
有4个实数根;若
,则
有2个实数根。
因此
总共有8个实数根,所以
有8个零点。
这种方法也揭示了做嵌套函数题目的本质——剥离分析,那么同样的,一题多解,我们再次考虑用我们的反函数画出曲线的方式来分析这个嵌套函数。
于是
就等价于
于是我们需要将
进行分段绘制其反函数,得到一个和
关于
对称的曲线,为了方便描述还是将其称之为
的图像。
因此如图所示
,再次强调一遍,由于反函数与原函数的定义域和值域发生了转变,因此反函数的定义域(
)对应着原函数的值域(
)。
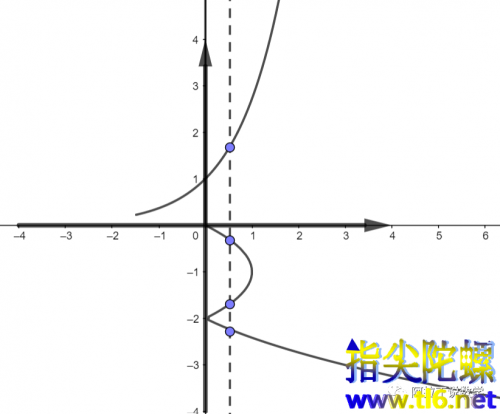
于是根据图像我们发现
也就是
与
的交点有4个,分别是
,其中
.
因此对应到原函数
当
时,
有2个交点;当
时,
有4个交点;当
时,
有1个交点;当
时,
有1个交点
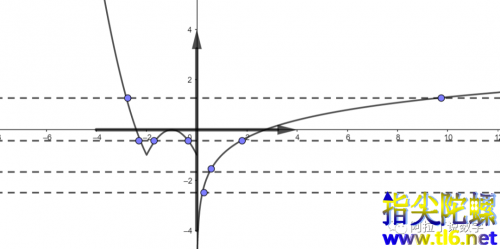
综上所述,一共有8个交点,于是
的零点有8个。
写在后面
不过还是要再强调一遍,我们在这里只是绘制了一种隐曲线,并不是严格的反函数,虽然这种方法不严格,但是这种数形结合的思想是值得我们学习的。
关于嵌套函数最朴实也是最本质的办法就是一次次剥离分析,但是在高考中数形结合的思想是亘古不变的,根据反函数的性质构造相应的曲线交点来辅助分析函数会使我们更快更准确的得到我们想要的答案。