手指速算法都要那些?手指速算法口诀大全
数学速算法指利用数与数之间的特殊关系进行较快的加减乘除运算。这种运算方法称为速算法,心算法。
速算法的分类有哪些?
快心算
速算一:快心算-----真正与小学数学教材同步的教学模式
快心算是目前唯一不借助任何实物进行简便运算的方法,既不用练算盘,也不用扳手指,更不用算盘。
快心算教材的编排和难度是紧扣小学数学大纲并于初中代数接轨,比小学课本更简便的一门速算。简化了笔算,加强了口算。简单,易学,趣味性强,小学生通过短时间培训后,多位数加,减,乘,除,不列竖式,直接可以写出答数。
快心算的神奇效果
三年级以上任意多位数的乘除加减全部学完。
二年级多位数的加减,两位数的乘法和一位数的除法。
一年级,多位数的加减。
幼儿园中,大班学会多位数加减法为学龄前幼儿量身定做的,提前渡过小学口算这一关。小孩在幼儿园学习快心算对以后上小学有帮助孩子们做作业不再用草稿纸,看算直接写答案.
袖里吞金
速算二:央视热播剧《走西口》里豆花多次夸田青会“袖里吞金”速算。(就是计算不借助算盘)!那究竟什么是袖里吞金速算法?
袖里吞金就是一种速算的方法,是我国古代商人发明的一种数值计算方法,古代人的衣服袖子肥大,计算时只见两手在袖中进行,固叫袖里吞金速算。这种计算方法过去曾有一段歌谣流传;“袖里吞金妙如仙,灵指一动数目全,无价之宝学到手,不遇知音不与传”。
袖里吞金速算法就是一种民间的手心算的方法,中国的商贾数学,晋商一面走路一面算账,,十个手指就是一把算盘,所以山西人平时总将一双手吞在袖里,怕泄露了他的经济秘密。过去人们为了谋生不会轻易将这种算法的秘笈外传,一种在中华大地上流传了至少400多年名叫“袖里吞金”的速算方式也濒临失传。
根据有关资料显示,公元1573年,一位名叫徐心鲁的学者,写了一本《珠盘算法》,最早描述了袖里吞金速算;公元1592年,一位名叫程大位的数学家,出版了一本《算法统筹》,首次对袖里吞金进行了详细描述。后来商人尤其是晋商,推广使用了这门古代的速算方法。“袖里吞金”算法是山西票号秘不外传的一门绝技,西安的一些大商家大掌柜的都会这种速算法。
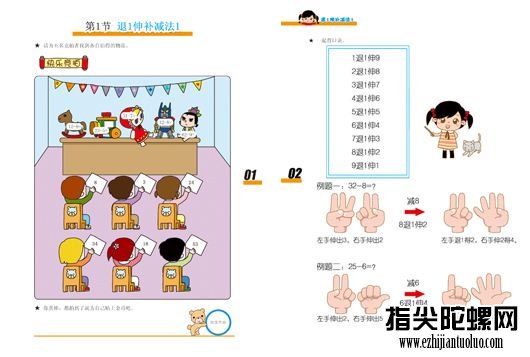
袖里吞金速算表示数的方法是以左手五指设点作为数码盘,每个手指表示一位数,五个手指可表示个、十、百、千、万五位数字。每个手指的上、中、下三节分别表示1-9个数。每节上布置着三个数码,排列的规则是分左、中、右三列,手指左边逆上(从下到上)排列1、2、3:手指中间顺下(从上到下)排列4、5、6:手指右边逆上排列7、8、9。袖里吞金的计算方法是采用心算办法利用大脑形象再现指算计算过程而求出结果的方法。它把左手当作一架五档的虚算盘,用右手五指点按这个虚算盘来进行计算。记数时要用右手的手指点左手相对应的手指。其明确分工是:右手拇指/专点左手拇指,右手食指专点左手食指,右手中指专点左手中指,右手无名指专点左手无名指,右手小指专点左手小指。对应专业分工各不相扰。哪个手指点按数,哪个手指就伸开,手指不点按数时弯屈,表示0。它不借助于任何计算工具,不列运算程序,只需两手轻轻一合,便知答数,可进行十万位以内的任意数的加减乘除四则运算。
袖里吞金’速算,其运算速度(当然要经过一定时间的练习),加减可与电子计算机相媲美,乘除比珠算要快,平方、开平方比笔算快得多。虽然对于初学者来说,用‘袖里吞金’计算简单的数据不如计算器快,但熟练掌握这项技能后,计算速度要超过计算器。曾经有人专门计算过‘袖里吞金’算法的速度,一个熟练掌握这门技能的人,得数结果为3到4位数的乘法,大约为2秒钟的时间;结果为5到7位数的,约为7秒钟左右;
袖里吞金速算法虽然脱胎于珠算,但与珠算相比,不需要任何的工具,只要使用一双手就可以了。由于“袖里吞金”不用工具、不用眼看等特点,非常适合在野外作业时使用,在黑暗中也可以使用,尤其是对于盲人,更可以通过这种算法来解决一些问题。“俗话说‘十指连心’,运用手指来训练计算技能,可以活动筋骨,心灵手巧,手巧促心灵,提高脑力。”
蒙氏速算
速算三:蒙氏速算是在蒙氏数学基础上的发展与创新,蒙氏数学相对低幼一点,而“蒙氏速算”是针对学前班孩子的,最大优势就是幼小衔接好,与小学数学计算方法一致。适合幼儿园中班大班小朋友及小学一二年级学生学习。
蒙氏速算能使幼儿在拼玩中,深刻理解数字计算的根本原理。从而轻松突破孩子的数学计算关,数字的计算蕴藏着包含,分类,分解合并,归纳,对称逻辑推理等抽象思维,而学前孩子只会图象思维,不会理解和推理,所以学前孩子学习计算是非常困难的。
蒙氏速算----算理简捷,与国家九年义务教育课程标准完全接轨,使4.5岁儿童在一个学期内,可学会万以内加减法的运算. 蒙氏速算从最基本的数概念入手一环扣一环,与小学数学计算方法一致。但教学方法简单,学生易学,易接受。蒙氏速算轻松快乐的教学,利用卡通,实物等数字形象,把抽象枯燥的数学概念形象化,把复杂的问题简单化。蒙氏速算是幼小衔接最佳数学课程,提高少儿数学素质的新方法。
有条件的特殊数的运算
两位数乘法速算技巧
原理:设两位数分别为10A+B,10C+D,其积为S,根据多项式展开:
S=(10A+B)×(10C+D)=10A×10C+B×10C+10A×D+B×D,而所谓速算,就是根据其中一些相等或互补(相加为十)的关系简化上式,从而快速得出结果。
注:下文中 “--”代表十位和个位,因为两位数的十位相乘得数的后面是两个零,请大家不要忘了,前积就是前两位,后积是后两位,中积为中间两位,满十前一,不足补零.
A.乘法速算
一.前数相同的:
1.1.十位是1,个位互补,即A=C=1,B+D=10,S=(10+B+D)×10+B×D
方法:百位为二,个位相乘,得数为后积,满十前一。
例:13×17
13+7=2--(“-”在不熟练的时候作为助记符,熟练后就可以不使用了)
3×7=21
-----------------------
221
即13×17=221
1.2.十位是1,个位不互补,即A=C=1,B+D≠10,S=(10+B+D)×10+A×B
方法:乘数的个位与被乘数相加,得数为前积,两数的个位相乘,得数为后积,满十前一。
例:15×17
15+7=22-(“-”在不熟练的时候作为助记符,熟练后就可以不使用了)
5×7=35
-----------------------
255
即15×17=255
1.3.十位相同,个位互补,即A=C,B+D=10,S=A×(A+1)×10+B×D
方法:十位数加1,得出的和与十位数相乘,得数为前积,个位数相乘,得数为后积
例:56×54
(5+1)×5=30--
6×4=24
----------------------
3024
1.4.十位相同,个位不互补,即A=C,B+D≠10,S=A×(A+1)×10+A×B
方法:先头加一再乘头两,得数为前积,尾乘尾,的数为后积,乘数相加,看比十大几或小几,大几就加几个乘数的头乘十,反之亦然
例:67×64
(6+1)×6=42
7×4=28
7+4=11
11-10=1
4228+60=4288
----------------------
4288
方法2:两首位相乘(即求首位的平方),得数作为前积,两尾数的和与首位相乘,得数作为中积,满十进一,两尾数相乘,得数作为后积。
例:67×64
6×6=36--
(4+7)×6=66-
4×7=28
----------------------
4288
二、后数相同的:
2.1. 个位是1,十位互补即 B=D=1,A+C=10S=10A×10C+101
方法:十位与十位相乘,得数为前积,加上101.。
--8×2=16--
101
-----------------------
1701
2.2.<不是很简便>个位是1,十位不互补即 B=D=1,A+C≠10S=10A×10C+10C+10A+1
方法:十位数乘积,加上十位数之和为前积,个位为1.。
例:71×91
70×90=63--
70+90=16-
1
----------------------
6461
2.3个位是5,十位互补即 B=D=5,A+C=10S=10A×10C+25
方法:十位数乘积,加上十位数之和为前积,加上25。
例:35×75
3×7+5=26--
25
----------------------
2625
2.4<不是很简便>个位是5,十位不互补即 B=D=5,A+C≠10S=10A×10C+525
方法:两首位相乘(即求首位的平方),得数作为前积,两十位数的和与个位相乘,得数作为中积,满十进一,两尾数相乘,得数作为后积。
例:75×95
7×9=63--
(7+9)×5=80-
25
----------------------------
7125
2.5. 个位相同,十位互补即 B=D,A+C=10S=10A×10C+B100+B2
方法:十位与十位相乘加上个位,得数为前积,加上个位平方。
例:86×26
8×2+6=22--
36
-----------------------
2236
2.6.个位相同,十位非互补
方法:十位与十位相乘加上个位,得数为前积,加上个位平方,再看看十位相加比10大几或小几,大几就加几个个位乘十,小几反之亦然
例:73×43
7×4+3=31
9
7+4=11
3109+30=3139
-----------------------
3139
2.7.个位相同,十位非互补速算法2
方法:头乘头,尾平方,再加上头加尾的结果乘尾再乘10
例:73×43
7×4=28
9
2809+(7+4)×3×10=2809+11×30=2809+330=3139
-----------------------
3139
三、特殊类型的:
3.1、一因数数首尾相同,一因数十位与个位互补的两位数相乘。
方法:互补的那个数首位加1,得出的和与被乘数首位相乘,得数为前积,两尾数相乘,得数为后积,没有十位用0补。
例: 66×37
(3+1)×6=24--
6×7=42
----------------------
2442
3.2、一因数数首尾相同,一因数十位与个位非互补的两位数相乘。
方法:杂乱的那个数首位加1,得出的和与被乘数首位相乘,得数为前积,两尾数相乘,得数为后积,没有十位用0补,再看看非互补的因数相加比10大几或小几,大几就加几个相同数的数字乘十,反之亦然
例:38×44
(3+1)*4=16
8*4=32
1632
3+8=11
11-10=1
1632+40=1672
----------------------
1672
3.3、一因数数首尾互补,一因数十位与个位不相同的两位数相乘。
方法:乘数首位加1,得出的和与被乘数首位相乘,得数为前积,两尾数相乘,得数为后积,没有十位用0补,再看看不相同的因数尾比头大几或小几,大几就加几个互补数的头乘十,反之亦然
例:46×75
(4+1)*7=35
6*5=30
5-7=-2
2*4=8
3530-80=3450
----------------------
3450
3.4、一因数数首比尾小一,一因数十位与个位相加等于9的两位数相乘。
方法:凑9的数首位加1乘以首数的补数,得数为前积,首比尾小一的数的尾数的补数乘以凑9的数首位加1为后积,没有十位用0补。
例:56×36
10-6=4
3+1=4
5*4=20
4*4=16
---------------
2016
3.5、两因数数首不同,尾互补的两位数相乘。
方法:确定乘数与被乘数,反之亦然。被乘数头加一与乘数头相乘,得数为前积,尾乘尾,得数为后积。再看看被乘数的头比乘数的头大几或小几,大几就加几个乘数的尾乘十,反之亦然
例:74×56
(7+1)*5=40
4*6=24
7-5=2
2*6=12
12*10=120
4024+120=4144
---------------
4144
3.6、两因数首尾差一,尾数互补的算法
方法:不用向第五个那么麻烦了,取大的头平方减一,得数为前积,大数的尾平方的补整百数为后积
例:24×36
3>2
3*3-1=8
6^2=36
100-36=64
---------------
864
3.7、近100的两位数算法
方法:确定乘数与被乘数,反之亦然。再用被乘数减去乘数补数,得数为前积,再把两数补数相乘,得数为后积(未满10补零,满百进一)
例:93×91
100-91=9
93-9=84
100-93=7
7*9=63
---------------
8463
B、平方速算
一、求11~19 的平方
同上1.2,乘数的个位与被乘数相加,得数为前积,两数的个位相乘,得数为后积,满十前一
例:17×17
17+7=24-
7×7=49
---------------
289
三、个位是5 的两位数的平方
同上1.3,十位加1 乘以十位,在得数的后面接上25。
例:35×35
(3+1)×3=12--
25
----------------------
1225
四、十位是5 的两位数的平方
同上2.5,个位加25,在得数的后面接上个位平方。
例: 53×53
25+3=28--
3×3=9
----------------------
2809
四、21~50 的两位数的平方
求25~50之间的两数的平方时,记住1~25的平方就简单了,11~19参照第一条,下面四个数据要牢记:
21×21=441
22×22=484
23×23=529
24×24=576
求25~50 的两位数的平方,用底数减去25,得数为前积,50减去底数所得的差的平方作为后积,满百进1,没有十位补0。
例:37×37
37-25=12--
(50-37)^2=169
--------------------------------
1369
C、加减法
一、补数的概念与应用
补数的概念:补数是指从10、100、1000……中减去某一数后所剩下的数。
例如10减去9等于1,因此9的补数是1,反过来,1的补数是9。
补数的应用:在速算方法中将很常用到补数。例如求两个接近100的数的乘法或除数,将看起来复杂的减法运算转为简单的加法运算等等。
D、除法速算
一、某数除以5、25、125时
1、被除数÷5
=被除数÷(10÷2)
=被除数÷10×2
=被除数×2÷10
2、被除数÷25
=被除数×4÷100
=被除数×2×2÷100
3、被除数÷125
=被除数×8÷1000
=被除数×2×2×2÷1000
在加、减、乘、除四则运算中除法是最麻烦的一项,即使使用速算法很多时候也要加上笔算才能更快更准地算出答案。因本人水平所限,上面的算法不一定是最好的心算法。