彭罗斯和他的图形:诡异的三角形、彭罗斯阶梯、彭罗斯瓷砖
彭罗斯不仅在数学物理领域的造诣深不可测,在趣味数学和哲学方面也有重要的影响。他曾经创造了一批“四维空间的图形”,意思就是说,这些图形在三维空间是不可能存在的。
诡异的三角形
你一定见过这样的三角形吧?它看起来像是一个固体,由三个截面为正方形的长方体所构成,三个长方体组合成为一个三角形,但两长方体之间的夹角似乎又是直角。

现实中,这样的三角形根本不存在,但它有一个名字,叫做“彭罗斯三角”。它是所有不可能图形中最基础、最著名的一个。
小时候,彭罗斯的父亲莱昂内尔·彭罗斯常常会给他出谜题和做玩具,启发他的动手能力,还给他修建了一间小木工棚。有一次,父亲做了12块不同的木楔,然后给出了组合规则,让他用各种复杂的方式把这些形状各异的木楔组合起来。正是这种训练,在很大程度上启发了他成年以后对空间几何的思考。
无限循环的阶梯
相信很多人都看过《盗梦空间》这部经典的电影。在电影里,在第二层梦境中,迪卡普里奥的助手列维特逃跑过程中突然发现无路可逃,他面对的楼梯处在无限死循环当中。
这种楼梯,叫“彭罗斯阶梯”,是彭罗斯的另一代表成就,一个著名的几何学悖论。1958年,他提出这个理论之后,他的朋友——荷兰画家莫里茨·埃舍尔对此很感兴趣,并充分利用彭罗斯阶梯,作了一幅画,叫做《上行和下行》,如下图:

从直观的视觉来看,彭罗斯阶梯就是由四条首尾相连接的阶梯构成,在这四条阶梯当中,你找不到最高的一点,也找不到最低的一点,它们可能始终都是向下或者向上,但永远都走不到头。
一旦走进彭罗斯阶梯就会迷失,一次又一次地回到原本的位置。从直观的角度来看,破解彭罗斯阶梯很简单,只要跳出阶梯就行了,但是身在其中,由于视觉受蒙蔽,你根本不知道该从哪里去破解。
彭罗斯阶梯在三维空间并不存在,它只会存在于二维世界或者更高阶的空间当中。自从这个彭罗斯阶梯被提出后,有不少的科学家试图去证实它的存在,但最终都失败了。
虽然三维现实中它并不存在,但是不少的影视作品都采用了彭罗斯阶梯的理论,除了《盗梦空间》出现的无限循环的楼梯,《盗墓笔记》当中也使用了彭罗斯阶梯的原理。
此外,彭罗斯阶梯似乎也可以用来解释人们常说的“鬼打墙”。一般来说,“鬼打墙”都是出现在夜晚或者郊外,人往往会因为“鬼打墙”总是在原地转圈。
在古代,一些术士会利用奇门八卦来破解它,即算出一条所谓的“生门”。而这种“生门”在科学界早就有了一种解释——
将人或者某个生物的眼睛蒙上,你会发现不管他们怎么走都只是一个圆圈,换句话说,生物的运动本能就是圆周运动。如果没有任何目标,他们就会自然而然地“绕圈”走,而生物之所以能够保持直线运动,是因为其眼睛在修正路线。古代风水术士在“寻龙定穴”时,也会布置一些标志物,摆一个阵,道理就在于人往往会依赖自己的视觉。
由此可见,眼见不一定为实,眼睛被蒙骗了,人就会迷失,这个灵异的“鬼打墙”在一定程度上,也是因为彭罗斯阶梯的原理。
永不重复的图案
彭罗斯在建筑界也是赫赫有名,因为他发明了“彭罗斯瓷砖”,改变了装潢的艺术。
“彭罗斯瓷砖”是一种非周期性镶嵌方式,它构成的图案非常神奇——就算铺满世界,图案也不会重复。
当时,他的画家朋友埃舍尔,对形似生物的形状进行“周期性镶嵌”而创作了许多图画,从而闻名遐迩。
所谓的周期性镶嵌,是指你可以描出一个区域的轮廓,通过平移这个区域就可以镶嵌整个平面,所谓平移就是在不通过旋转或者翻转的情况下移动这个区域的位置。例如,在埃舍尔的一幅代表作中(下图),一对毗连的黑鸟和白鸟构成了一个平移镶嵌的基本区域。想象这个平面上蒙着一层透明的纸,纸上描出了每片镶嵌片的轮廓。只有在镶嵌方式为周期性时,你才能在不通过旋转的情况下将这张纸移动到一个新的位置,使得所有轮廓都再次恰好相符。

埃舍尔一直认为通过各种各样的平移和反射,一幅镶嵌图案可以无限期地继续下去。然而,当彭罗斯送给他一套自己制作的木板拼图时,却彻底改变了他的这种想法。
彭罗斯送给他的拼图是这样的:基本图形只有一个——一个菱形的变形图案。菱形的两条边被切割出一个60°/120°的梯形形状,如图所示。然后让他把这些图形随意拼合形成一幅镶嵌图案。
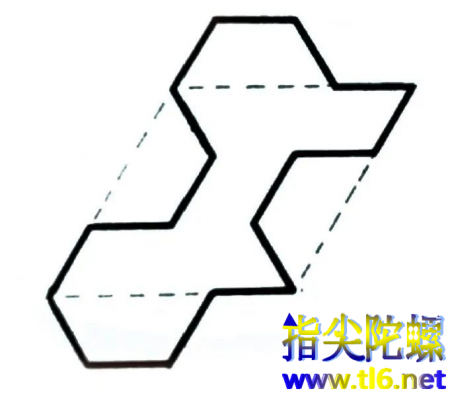
据说埃舍尔最终花费了几个星期,才非常惊讶地发现只有一种独特的方式可以将它们全部组合起来,而且它的图案是非周期性的,完全不重复,与他之前的认识完全不同。
在这之后,彭罗斯又发明了一种只有两种基本形状的非周期性镶嵌方案。他称这两个图案为飞镖(右)和风筝(左)。它们通过最明显的方式就能拼在一起,形成一个菱形。
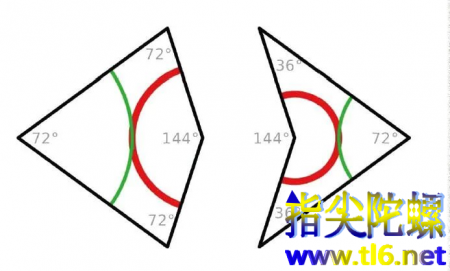
但是,如果你想创造一个非周期性镶嵌,就不能以这种方式拼接。上图中的弧线指示了拼接规则:弧线段必须连在一起。后来人们发现,这些非周期性的镶嵌可以通过第二种形状来创建:一个锐角菱形和一个钝角菱形,角度分别为(36°,144°)(上图左)和(72°,108°)(上图右),即所有的角的度数必须是36的倍数。在彭罗斯拼图中,飞镖与风筝的比例以及锐角与钝角的比例总是相同的,这个数值就是黄金分割比例——1:1.618。换句话说,如果一个彭罗斯拼图包含100个飞镖,它将包含162个风筝。数字越大,比率越接近黄金分割比率。
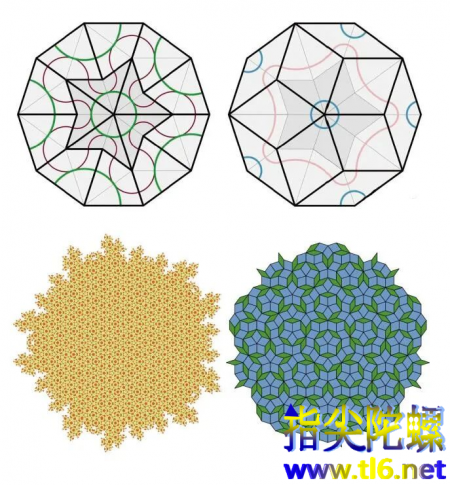
“彭罗斯瓷砖”最初的价值更多体现于实用美学,但后来人们终于发觉,这种镶嵌的三维形式正是物质的新形态基元,现代晶体学所热衷于探讨的“准晶体”便需要借助于“彭罗斯点阵”的思想方法来构造。